
- •Задания к контрольной работе (матанализ ч. 2) для заочников.
- •Тематический план.
- •Перечень заданий. Неопределенный интеграл функции одной переменной
- •Дифференциальное исчисление функции двух переменных
- •Геометрические приложения определенного интеграла
- •Примеры
- •Функции многих переменных Частные производные. Геометрическая интерпретация частной производной.
- •Теоремы о дифференцируемых фмп.
- •Экстремумы фмп.
- •Примеры
Задания к контрольной работе (матанализ ч. 2) для заочников.
Выбор темы контрольной работы: выбирается по первой букве фамилии студента и последней цифре номера зачетной книжки.
|
А Е Л Р Х Э |
Б Ж М С Ц Ю |
В З Н Т Ч Я |
Г И О У Ш |
Д К П Ф Щ
|
1 |
|
|
|
|
|
2 |
|
|
|
|
|
3 |
|
|
|
|
|
4 |
|
|
|
|
|
5 |
|
|
|
|
|
6 |
|
|
|
|
|
7 |
|
|
|
|
|
8 |
|
|
|
|
|
9 |
|
|
|
|
|
0 |
|
|
|
|
|
Тематический план.
Тема 1. Неопределённый интеграл.
Тема 2. Определённый интеграл.
Тема 3. Дифференциальные уравнения.
СОДЕРЖАНИЕ КУРСА.
Тема 1. Первообразная функции и неопределённый интеграл. Основные свойства неопределённого интеграла. Интегралы основных элементарных функций. Интегрирование путём замены переменной. Метод интегрирования по частям. Интегрирование простейших рациональных дробей. Интегрирование тригонометрических функций.
Тема 2. Определённый интеграл и его свойства. Теорема о существовании определённого интеграла. Интеграл с переменным верхним пределом. Формула Ньютона-Лейбница. Методы замены переменной и интегрирование по частям в определённом интеграле. Геометрические приложения определённого интеграла. Несобственные интегралы. Приближённое вычисление определённых интегралов.
Тема 3. Дифференциальные уравнения первого порядка. Дифференциальные уравнения с разделяющимися переменными. Линейные дифференциальные уравнения. Уравнения Бернулли. Линейные дифференциальные уравнения с постоянными коэффициентами.
Перечень заданий. Неопределенный интеграл функции одной переменной
Вычислить
неопределенный интеграл методом
непосредственного интегрирования ( – произвольные константы, не равные
нулю). Сделать проверку (посредством
дифференцирования).
– произвольные константы, не равные
нулю). Сделать проверку (посредством
дифференцирования).
№ |
Неопределенный интеграл |
1 |
|
2 |
|
3 |
|
4 |
|
5 |
|
6 |
|
7 |
|
8 |
|
9 |
|
10 |
|
11 |
|
12 |
|
13 |
|
14 |
|
15 |
|
16 |
|
17 |
|
18 |
|
19 |
|
20 |
|
21 |
|
22 |
|
23 |
|
24 |
,
|
25 |
|
26 |
|
27 |
|
28 |
|
29 |
,
,
|
30 |
|
31 |
,
|
32 |
|
33 |
|
34 |
|
35 |
|
36 |
|
37 |
|
38 |
|
39 |
|
40 |
|

 ,
,
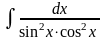 ,
,
 ;
; ,
,
 ,
,
 ;
; ,
,
 ,
,
 ;
; ,
,
 ,
,
 ;
; ,
,
 ,
,
 ;
; ,
,
 ,
,
 ;
; ,
,
 ,
,
 ;
; ,
,
 ,
,
 ;
;
 ,
,
 ,
,
 ;
; ,
,
 ,
,
 ;
;
 ,
,
 ,
,
 ;
;
 ,
,
 ,
,
 ;
;
 ,
,
 ,
,
 ;
;
 ,
,
 (указание: несколько раз воспользоваться
формулой
(указание: несколько раз воспользоваться
формулой
 ),
),
 ;
; ,
,
 ,
,
 ;
;
 ,
,
 ,
,
 ;
;
 ,
,
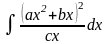 ,
,
 ;
;
 ,
,
 ,
,
 (указание: воспользоваться два раза
формулой понижения степени
(указание: воспользоваться два раза
формулой понижения степени
 );
);
 ,
,
 ,
,
 ;
;
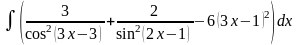 ,
,
 ,
,
 ;
;
 ,
,
 ,
,
 ;
;
 ,
,
 ,
,
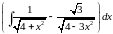 ;
;
 ,
,
 ,
;
,
;
 ,
;
,
;
 ,
,
 ,
,
 ;
;
 ,
,
,
,
 ;
;
 ,
,
 ,
,
 ;
;
 ,
,
 ,
,
 ;
;
 ;
;
 (указание:
воспользоваться формулой
),
(указание:
воспользоваться формулой
),
 ,
;
,
;
 ,
, ;
;
 ,
,
 ,
,
 ;
; ,
,
 ,
;
,
;
 ,
,
 ,
, ;
;
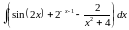 ,
,
 ,
,
 ;
;
 ,
,
 ,
,
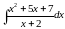 ;
;
 ,
,
 ,
, ;
;
 ,
,
 ,
,
 ;
; ,
,
 ,
,
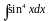 (указание: воспользоваться два раза
формулой понижения степени
(указание: воспользоваться два раза
формулой понижения степени
 );
);
 ,
,
 ,
,
 .
.