
- •2. Аксиомы стереометрии
- •3. Способы задание плоскости
- •4. Взаимное расположение прямых в пространстве
- •5. Параллельность прямой и плоскости
- •6. Параллельность плоскостей
- •7. Перпендикулярность прямой и плоскости
- •7.1. Определение
- •7.2. Свойства перпендикулярных прямой и плоскости
- •8. Перпендикуляр и наклонная
- •9. Расстояние в стереометрии
- •10. Перпендикулярные плоскости
- •11. Углы между прямыми и плоскостями
- •11.1. Угол между скрещивающимися прямыми
- •11.2. Угол между прямой и плоскостью
- •11.3. Угол между плоскостями
4. Взаимное расположение прямых в пространстве
Как известно из планиметрии, для двух прямых на плоскости возможны лишь два случая их взаимного расположения: либо эти прямые пересекаются, либо они параллельны. Поскольку в пространстве имеются плоскости и на них выполняется планиметрия, то эти два случая взаимного расположения двух прямых сохраняются и для пространства. Но в пространстве добавляется еще один случай – когда две прямые не лежат в одной плоскости.
Две прямые, не лежащие в одной плоскости, называются скрещивающимися. Иначе говоря, скрещивающиеся прямые – это такие прямые, через которые нельзя провести плоскость.
Итак, для взаимного расположения двух прямых в пространстве имеются только три исключающие друг друга возможности:
Две прямые лежат в одной плоскости и имеют общую точку – пересекающиеся прямые.
Две прямые лежат в одной плоскости и не имеют общих точек; такие прямые, как и в планиметрии, называются параллельными.
Две прямые не лежат в одной плоскости – скрещивающиеся прямые.
Скрещивающиеся прямые не имеют общей точки, так как в противном случае в силу теоремы 2 они лежали бы в одной плоскости.
Две прямые в пространстве имеют не более одной общей точки, они имеют либо одну общую точку, либо не имеют ни одной.
В дальнейшем будет встречаться такая ситуация, когда для двух данных прямых требуется решить вопрос об их взаимном расположении, но нельзя непосредственно сослаться на соответствующие определения. В этом случае удобно пользоваться признаками. Сформулируем два признака скрещивающихся прямых:
если две прямые содержат четыре точки, не лежащие в одной плоскости, то они скрещиваются;
прямая, пересекающая плоскость, скрещивается с каждой прямой, лежащей в этой плоскости и не проходящей через точку пересечения заданной прямой и плоскости.
5. Параллельность прямой и плоскости
Прямая и плоскость называются параллельными, если они не пересекаются.
Теорема 5.1. Если прямая, не принадлежащая плоскости, параллельна какой-нибудь прямой в этой плоскости, то она параллельна и самой плоскости.
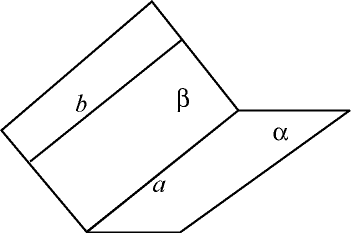
Доказательство. Пусть – плоскость, – не лежащая в ней прямая и – прямая в плоскости , параллельная прямой . Проведем плоскость через прямые и . Плоскости и пересекаются по прямой . Если бы прямая пересекала плоскость , то точка пересечения принадлежала бы прямой . Но это невозможно, так как прямые параллельны. Итак, прямая не пересекает плоскость , а значит, параллельна плоскости ей.
Теорема 5.2. Если плоскость проходит через прямую, параллельную другой плоскости, то линия пересечения этих плоскостей параллельна данной прямой.

Доказательство. Пусть прямая параллельна плоскости и принадлежит плоскости . Докажем что прямая пересечения плоскостей и - - параллельна прямой . Предположим, что это не так. Тогда прямые и пересекаются, но поскольку прямая лежит в плоскости , значит прямая пересекает , что противоречит условию их параллельности, следовательно и параллельны.
Теорема 5.3. Если через каждую из двух параллельных прямых провести плоскость, причем эти плоскости пересекаются, то линия их пересечения параллельна каждой из данных прямых.

Доказательство.
![]()
![]() .
По условию
значит по Теореме 5.1
.
По условию
значит по Теореме 5.1
![]() .
Так как к тому же
,
значит по Теореме 5.2
.
Так как к тому же
,
значит по Теореме 5.2
![]() .
Аналогично доказывается, что
.
Аналогично доказывается, что
![]() .
.
Теорема 5.4. Две прямые, параллельные третьей прямой, параллельны между собой.
