5. Вынужденные электрические колебания. Полное сопротивление цепи с с, l и к. Дифференциальное уравнение вынужденных колебаний и его решение???
Колебания, возникающие в CLR-цепочке при наличии переменной э.д.с., называются вынужденными.Эту э.д.с. нужно прибавить к э.д.с. самоиндукции, в результате уравнение из предыдущей темы примет вид Ld2q/dt2 +Rdq/dt + q/C = Е0cosωt. Вынужденные колебания электрического заряда в цепи контура определяются q=qmcos(ωt - ψ),где ψ – сдвиг фаз между внешней э.д.с. и напряжением (зарядом) на конденсаторе, а tg ψ = R/(1/ωC–ωL). Установившиеся вынужденные колебания.Продифференцировав выражение по переменной t, получим выражение для силы тока в контуре при установившихся колебаниях
I = - ωqm sin(ω0t - ψ) = Im cos(ω0t - ψ + π/2). Это выражение можно записать в виде
I = Im cos(ωt - φ),где φ = ψ – π/2 – сдвиг по фазе между током и приложенной э.д.с., а tgφ = tg(ψ – π/2) = - 1/tgψ = (ωL -1/ωC)/R
Im = E0/√R2 + (ωL – 1/ωC)2, где RL = ωL – реактивное индуктивное сопротивление, RC = 1/ωC – реактивное емкостное сопротивление, Х = ωL – 1/ωC – реактивное сопротивление,
Z = √R2 + (ωL – 1/ωC)2 – полное сопротивление цепи.
6. Резонанс напряжений и резонанс токов.
Резонанс напряжений. В цепи переменного тока, с последовательно включенными L, C и R, полное сопротивление контура имеет минимальное значение Zmin = R, если ωL = 1/ωC. В этом случае ток в цепи определяется этим сопротивлением, принимая максимальные значения (возможные при данном Um), что свидетельствует о наличии резонансной частоты ωрез для тока, значение которой определяется по условию ωL = 1/ωC, откуда ωрез = 1/√LC = ω0
т.е. резонансная частота для силы тока равна частоте собственных колебаний в контуре. Напряжение на R равно внешнему напряжению, приложенному к цепи (UR =U).
Это явление называется резонансом напряжений (последовательным резонансом) – резкое возрастание амплитуды силы тока в контуре с последовательно включенными L, C, R и Е при
ωрез = 1/√LC = ω0. В случае резонанса напряжений (UL)рез = (UС)рез.
Подставив в эту формулу значения резонансной частоты и амплитуды напряжений на катушке индуктивности и конденсаторе получим (UL)рез = (UС)рез = Im √L/C = (Um/R)√L/C = QUm,
где Q – добротность контура. Добротность контура определяет остроту резонансных кривых. Так как Q обычных колебательных контуров больше единицы, то (UL)рез = (UС)рез > Е, т.е. добротность показывает, во сколько раз напряжение на конденсаторе (катушке) больше напряжения приложенного к цепи.
Е = E0cos ωрезt, Iрез = (E0/R)cos ωрезt, I0max = E0/R.
Резонанс токов. Рассмотрим цепь переменного тока, содержащую параллельно включенные L и С, R = 0.
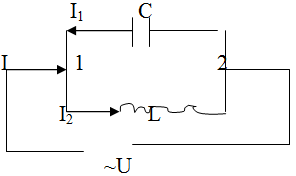
Если приложенное напряжение изменяется по закону U =Umcosωt, то в ветви 1С2 течет ток I1 = Im1cos(ωt–φ1), φ1 = (2n+3/2)π, n=1, 2, 3, ... амплитуда которого при условии L = 0 и R = 0: Im1 = Um/(1/ωC).
Аналогично, сила тока в цепи 1L2 I2 = Im2cos(ωt–φ2), φ2 = (2n+1/2)π, n=1, 2, 3, ... амплитуда которого при условии R = 0 и С=∞ (условие отсутствия емкости в цепи): Im2 = Um/(ωL).
Cравнив видим, что φ2 - φ1 =π, т.е. токи в ветвях противоположны по фазе. Амплитуда тока во внешней (неразветвленной) цепи Im = | Im1 - Im2 |= Um|ωC – 1/(ωL)|. Если ω = ωрез = 1/√(LС), то Im1 = Im2 и Im = 0.
Явление резкого уменьшения амплитуды силы тока во внешней цепи, питающей параллельно включенные конденсатор и катушку индуктивности, при приближении частоты ω приложенного напряжения к резонансной частоте ωрез называется резонансом токов (параллельным резонансом).
Амплитуда тока оказалась равной нулю, так как считали, что активное сопротивление контура R = 0. При R ≠ 0 разность фаз φ2 - φ1 ≠ π, поэтому Im ≠ 0 и сила тока I в подводящих проводах примет наименьшее возможное значение, обусловленное только током через резистор. При резонансе токов силы токов I1 и I2 могут значительно превышать силу тока I.Рассмотренный контур оказывает большое сопротивление переменному току с частотой, близкой к резонансной. Поэтому его свойства используются в резонансных усилителях, позволяющих выделить одно определенное колебание из сигнала сложной формы.