4. Свободные электромагнитные колебания в lс-контуре. Свободные затухающие колебания. Добротность контура. Дифференциальное уравнение затухающих колебаний и его решение.

Электромагнитными колебаниями называются переодические изменения во времени значений силы тока и напряжения в электрической цепи, а также обусловленные этим взаимосвязанные колебания электрического и магнитного полей, которые описывают соответственно векторы Е и Н.

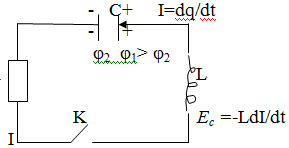
Если сопротивление R мало (R→0) электрический контур является идеальным (LC – контур). При R≠0 часть электрической энергии будет расходоваться на нагревание проводников и будет наблюдаться затухание колебательных процессов.

Свободные колебания в LC-контуре. Колебания электрического тока в контуре можно вызвать, либо сообщив обкладкам конденсатора некоторый начальный заряд, либо возбудив в индуктивности ток. Воспользуемся первым способом. При разомкнутом ключе зарядим конденсатор. Между обкладками конденсатора возникнет электрическое поле, энергия которого W_C = q²/2C. После замыкания ключа К емкость начнет разряжаться и в контуре потечет электрический ток. В результате энергия электрического поля будет уменьшаться, зато возникнет и начнет

увеличиваться энергия магнитного поля, обусловленного током, текущим через индуктивность. Энергия магнитного поля W_L=LI²/2. После этого те же процессы начнут протекать в обратном направлении, контур вернется в исходное состояние и весь цикл повторится снова и снова. Колебания электрического тока (заряда, напряжения) сопровождаются взаимными превращениями энергий электрического и магнитного полей.Будем обходить контур против часовой стрелки. При возрастании значения заряда на положительно заряженной обкладке конденсатора сила тока I = dq/dt.

Для расчета электрической цепи запишем закон Ома IR = φ₁ – φ₂ + E_C ; φ₁ – φ₂ =q/C, а э.д.с. самоиндукции E_c =-LdI/dt, то в виде дифференциального уравнения второго порядка по отношению к заряду q=q(t): Ld²q/dt² +Rdq/dt + q/C = 0 . Если учесть, что R = 0 , ω₀ = 1/√LC , то d²q/dt² + ω₀²q = 0 Решением уравнения является функция q = q_mcos(ω₀t + α).Выражение для периода колебаний (формула Томсона): T = 2π√(LC)

Используя известную формулу q = UC запишем выражение для напряжения на конденсаторе:

U = (1/C)q_mcos(ω₀t + α) = U_m cos(ω₀t + α).

Продифференцировав функцию по времени, получим выражение для силы тока в контуре: I = - ω₀q_m sin(ω₀t + α) = I_m cos(ω₀t + α + π/2).

U_m=q_m/C, I_m = ω₀q_m, U_m = I_m√(L/C)

Свободные затухающие колебания. Поскольку всякий реальный контур обладает активным сопротивлением R≠0, то введя обозначение β=R/(2L)

d²q/dt² + 2βdq/dt + ω₀²q = 0 это дифференциальное уравнение свободных затухающих колебаний.При условии, что β<ω₀ решение уравнения для заряда q имеет вид затухающих колебаний: q = q_m e^-βt cos(ωt + α), где ω = √( ω₀² – β²) - частота затухающих колебаний.

ω = √(1/LC – R²/4L²)

Колебания заряда на обкладках конденсатора происходят с периодом Т = 2π/ω и убывающей амплитудой q_m (t) = q_mexp(-Rt/2L).Напряжение на конденсаторе пропорционально заряду q, поэтому оно изменяется синхронно с зарядом q, а сила I = I_me^-βtcos(ωt + α +Δ) видно, что сила тока также затухает со временем, однако колебания тока происходят с некоторым опережением по фазе (Δ) относительно колебания заряда (напряжения) на конденсаторе.

Колебательный контур часто характеризуют его добротностью .Видно, что добротность контура тем больше, чем большее число колебаний он успевает совершить, прежде чем амплитуда колебаний уменьшиться в е раз. В случае слабого затухания Q = (1/R)√(L/C).