
- •1. Информация
- •Количество информации
- •Примеры решения задач с равновероятными возможностями
- •Тестовые задачи
- •Представление числовой информации
- •1.3. Представление символьной информации
- •1.4. Представление графической информации
- •2. Технические средства реализации информационных процессов
- •2.1. Основные этапы развития информатики и вычислительной техники
- •2.2. Состав и назначение основных элементов персонального компьютера
- •2.3. Устройства ввода (вывода)
- •3. Программные средства реализации информационных процессов
- •4. Модели решения функциональных и вычислительных задач
- •4.1. Основы логики
- •Тестовые задачи
- •4.2. Таблицы истинности. Логические схемы
- •Построим таблицу:
- •Логические схемы
- •Тестовые задачи
- •Тестовые задачи Упростить выражения:
- •Тестовые задачи
- •5. Алгоритмизация и программирование
- •6. Программное обеспечение и технологии программирования
- •7. Электронные таблицы
- •8. Базы данных
- •9. Локальные и глобальные сети
- •10. Основы защиты информации
Логические схемы
Из трех логических операций конъюнкции, дизъюнкции и инверсии (отрицания), выполняемых соответствующими элементами конъюнктром, дизъюнктром и инвертором, можно реализовать любые логические выражения.
А 1 1 0 0 |
В 1 0 1 0 |
Результат 1 0 0 0 |
А 1 1 0 0 |
В 1 0 1 0 |
Результат 1 1 1 0 |
А 1 0 |
0 1 |
Конъюнктор |
Дизъюнктор |
Инвертор |
|||||
|
|
|
|||||
Построение логических схем
Правило построения логических схем:
Определить число логических переменных;
Определить количество логических операций и их порядок;
Изобразить для каждой логической операции соответствующий ей вентиль;
Соединить вентили в порядке выполнения логических операций.
П
4.5. Пусть Х
= истина, Y
= ложь. Составить логическую схему для
следующего логического выражения: F
= X
![]() Y
Y
![]() X.
X.
Две переменные – X и Y;
Две логические операции: 2 1
X Y X;
Строим схему:


Ответ: 1 V 0 Λ 1 = 1.
П
4.6. Построить
логическую схему, соответствующую
логическому выражению
F
= X
Y
![]()
![]() .
Вычислить
значения выражения для Х
= 1, Y
= 0.
.
Вычислить
значения выражения для Х
= 1, Y
= 0.
Переменных две: Х и Y;
Логических операций три: конъюнкция и две дизъюнкции: 1 4 3 2
X
Y
![]() ;
;
Схему строим слева направо в соответствии с порядком логических операций:

Вычислим значение выражения: F = 1 0
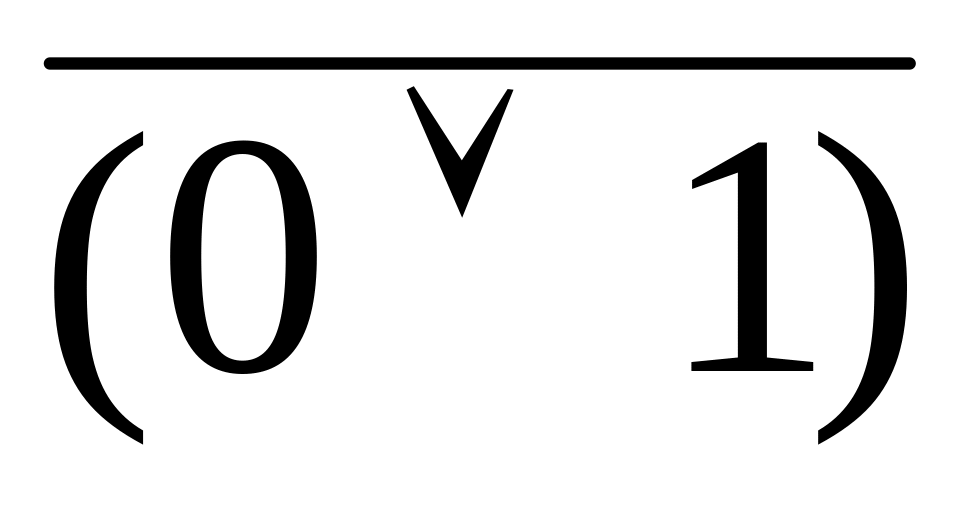 = 0.
= 0.
Тестовые задачи
Т 4.9. Составьте таблицы истинности для следующих логических выражений:
F = (X
 )
Z.
)
Z.F = X Y X.
F =
 (Y
X).
(Y
X).F =
 (Z
Λ Y).
(Z
Λ Y).
Т 4.10. Для какого из указанных значений числа X истинно высказывание:
(X > 4) \/ ((X > 1) → (X > 4))?
а) 1; б) 2; в) 3; г) 4.
Т 4.11. Постройте логическое выражение по логической схеме:
а
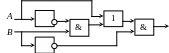 )
б)
)
б)


в) г)
Законы логики
Рассмотрим 6 законов логики и преобразование импликации:
1) коммутативность: A B=B A , A B = B A;
2) ассоциативность: A (B C) = (A B) C,
A (B C) = (A B) C;
3)
отрицание
операнда:
A
=F
,
A=T
,
![]() =A
,
=A
,
![]() =T;
=T;
4) дистрибутивность: A (B C) = (A B) (A C),
A (B C) = (A B) (A C);
5) поглощения операнда
A (A B) = A (A B) = А;
6) отрицание формулы (законы де Моргана):
![]() .
.
преобразование импликации
A B = B.
Законы логики часто используют для упрощения логического выражения.
П
4.7. Упростить
логическое выражение
![]() .
.
1) Избавимся от отрицания, используя закон 6 де Моргана
![]() ;
;
2)
Применим закон поглощения операнда к
формуле
![]() ,
тогда
,
тогда
![]() .
.
П 4.8. Упростить логическое выражение F = (A→B) (B→A).
1) Избавимся от импликации (A→B) и (B→A), используя преобразование 7
(A→B)
(B→A)
=
![]() ;
;
2)
Сгруппируем
![]() и применим закон 3 отрицания операнда
и применим закон 3 отрицания операнда
![]() .
.



