3.2. Основные формулы и законы постоянного магнитного поля
Магнитное поле
характеризуется напряженностью
и вектором магнитной индукции
,
,
(3.14)
где
- абсолютная магнитная проницаемость
среды. Для произвольной среды
,
где
- относительная магнитная проницаемость.
Единица напряженности
магнитного поля
-
.
В отличие от
электростатического поля, в котором
,
в магнитном поле
,
(3.15)
Величину
называют потоком вектора индукции через
поверхность S.
Размерность потока измеряется в веберах,
.
Поток равен 1 веберу, если при равномерном
его убывании до нуля в контуре возникает
ЭДС в 1в.
Поток через
замкнутую поверхность
,
так как магнитных зарядов одного знака
в природе нет (равенство Гаусса-Остроградского).
Закон Био-Савара
Этот закон гласит,
что напряженность магнитного поля
,
создаваемая током с плотностью
в объеме
равна
.
(3.16)
Рис. 3.3. К закону Био-Савара
Здесь
- векторное произведение векторов
и
,
которое равно
.
По абсолютной величине
,
где
-
угол между векторами
и
.
Из этой формулы видно, что максимальная
напряженность поля имеет место при
и равна нулю, если
совпадает с осью тока.
Естественно, что результирующая напряженность поля
.
(3.17)
Если это обычный проводник, то
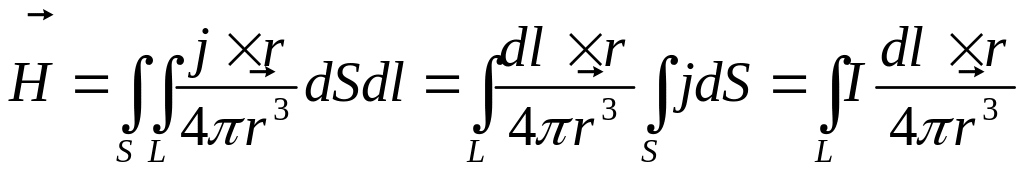(3.18)
Циркуляция магнитного поля
Циркуляцией напряженности магнитного поля называется интеграл по замкнутому контуру
.
(3.19)
Если бы существовало понятие магнитного заряда по аналогии с электрическим зарядом, то интеграл (6.5) определял бы величину работы поля, выполняемой при перемещении такого магнитного заряда по этому пути.
В электрическом поле аналогичная циркуляция равна нулю, то есть
.
В поле постоянных магнитов циркуляция напряженности магнитного поля также равно нулю. Не равна нулю циркуляция постоянного магнитного поля лишь в том случае, когда замкнутый контур охватывает пронизывающий его ток.
В общем случае
,
(3.20)
то есть циркуляция
напряженности магнитного поля равна
сумме токов, пронизывающих поверхность,
охваченную замкнутым контуром
(закон полного тока).
Нетрудно доказать, что, если контур не
охватывает ток, то
.
Ротор вектора
Понятие циркуляции позволяет определять интегральные характеристики поля. Понятие ротора позволит определить эти характеристики в дифференциальной форме, которые дадут возможность описывать поля в каждой отдельной точке пространства, точнее в некотором бесконечно малом объеме, окружающем эти точки.
Ротор вектора
- это вектор
,
,
(3.21)
такой что, его проекция в заданной точке пространства на нормаль к некоторой произвольной плоской площадке определяется выражением
,
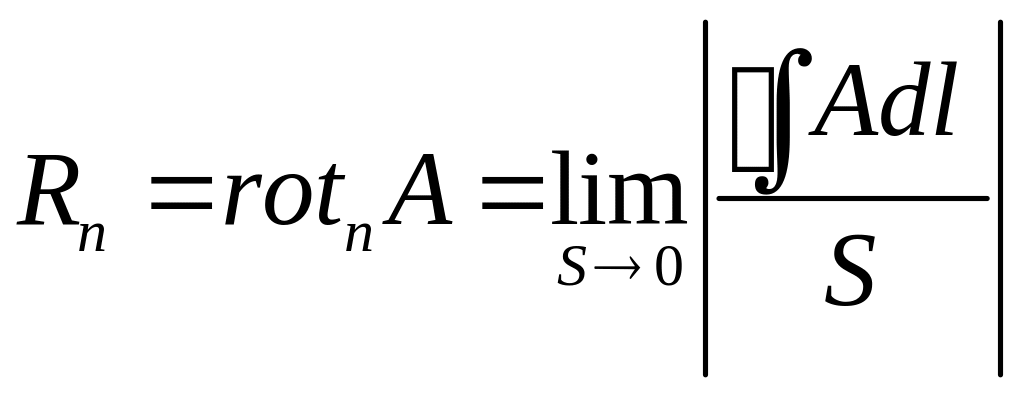(3.22)
где
- циркуляция вектора
по замкнутому контуру, охватываемому
заданную точку на площадке, ориентация
которой задана вектором нормали
(рис.3.4);
S – площадь, охваченная замкнутым
контуром интегрирования. В пределе эта
площадь устремляется к нулю. Естественно,
что для одного и того же вектора
можно
выбрать бесконечное число таких площадок
с различными ориентациями вектора
нормали
.
Соответственно и проекции
будут различны.
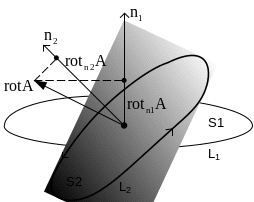
Рис. 3.4. К определению ротора
Поскольку в трехмерном пространстве вектор характеризуется тремя координатами, для полного описания вектора достаточно найти три его проекции на оси координат x,y,z. Соответственно, площадки в окрестности заданной точки должны быть перпендикулярны этим осям.
В результате имеем
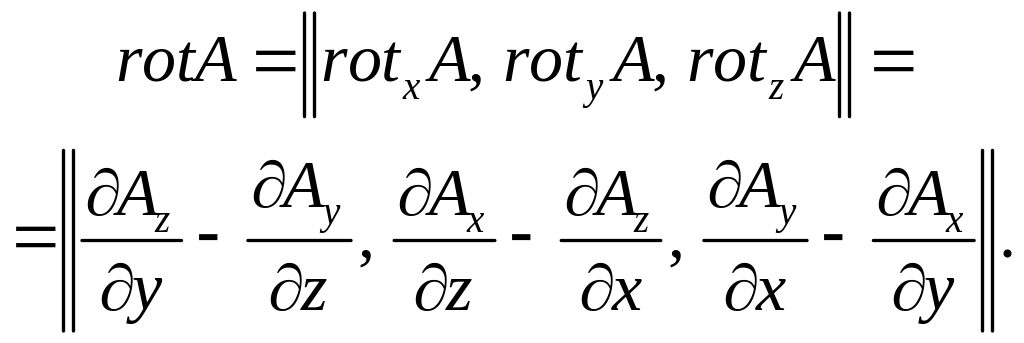(3.23)