
- •1.Основные понятия теории вероятностей. Классическое, статистическое и геометрическое определения вероятности. Основные понятия тв.
- •Статистическое определение вероятности
- •Геометрическое определение вероятности
- •2. Алгебраические операции над событиями. Отношение м/д событиями. Аксиоматическое определение вероятности события. Отношение м/д событиями
- •Аксиоматическое определение вероятностей события
- •3.Основные свойства вероятностей. Правило сложения вероятностей. Условные вероятности. Теорема умножения вероятностей. Независимые события.
- •4.Формула полной вероятности. Формула Байеса.
- •5.Повторение испытаний. Формула Бернулли.
- •6.Локальная и интегральная теоремы Лапласа.
- •7. Вероятность отклонения относительной частоты от постоянной вероятности в независимых испытаниях.
- •8. Наивероятнейшее число появлений события при повторных испытаниях по схеме Бернулли.
- •9. Случайные величины. Закон распределения вероятностей. Биноминальное распределение. Геометрическое распределение.
- •10. Распределение Пуассона.
- •11. Функция распределения св и ее свойства.
- •12. Непрерывные св. Равномерный закон распределения.
- •13 Показательный закон распределения. Нормальный закон распределения.
- •14 Многомерные случайные величины. Ф-ция распределения многомерной случайной величины, её свойства.
- •15 Двумерные непрерывные св. Плотность распределения вероятностей двумерной св, её свойства
- •16 Двумерные св. Условные законы распределения.
- •17 Независимые случайные величины. Критерий независимости.
- •18 Функции случайных величин, их законы распределения.
- •19.Числовые характеритики св.
- •20.Моменты распределения одномерной св.
- •21.Ковариация и коэффициент линейной корреляции 2 св, их свойства.
- •22.Условное мат ожидание
- •23. Двумерное нормальное распределение. Условие независимости некоррелированных св.
- •24.Теорема об условных распределениях компанент двумерной нормально распределенной св.
- •25 Характеристические функции случайных величин, их свойства. Примеры
- •26. Неравенства Маркова и Чебышева.
- •27. Теорема Чебышева. Теорема Маркова.
- •28. Центральная предельная теорема.
- •29. Теорема Ляпунова. Интегральная теорема Лапласса.
- •30. Распределение выборки. Эмпирическая функция распределения.
- •33. Оценка дисперсии случайной величины.
- •34. Неравенство Рао-Крамера. Следствие для несмещенной оценки
- •35. Эффективная оценка мат. Ожидания нормальной распределенной величины.
- •36. Асимптотически эффективные и сверх эффективные оценки. Теорема о состоятельности оценки.
- •37. Условные законы распределения. Условное мат. Ожидание.
- •38.Достаточные статистики. Критерий факторизации
- •39.Теорема Колмагорова – Блекуэлла.
- •41. Метод моментов
- •42. Распределение….
- •43. Распределение Стьюдента.
- •44. Теоремы о случайной величине, имеющей распределение Стьюдента.
- •45. Распределение Фишера. Теорема о случайной величине, имеющей распределение Фишера
- •46 Доверительный интервал для мат. Ожидания нормально распределенной с.В.( -неизвестно)
- •47 Доверительный интервал для мат. Ожидания нормально распределенной с.В.( -известно)
- •48 Доверительный интервал для дисперсии нормально распределеннной с.В.
- •55 Проверка гипотезы о равенстве двух дисперсий нормально распределенный с.В.
23. Двумерное нормальное распределение. Условие независимости некоррелированных св.
Опр.Двумерная СВ (Х,У) имеет нормальное распределение, если её плотность вероятности имеет вид:

δх ,δу положительные параметры и | ρ | <1.
Двумерное нормальное распределение СВ (Х,У) зависит от 5 параметров: mх , mу, δх ,δу ,ρ
Если СВ Х и У распределены нормально , то М(х)= mх, М(у)= mу.
Если rху= 0 , то СВ не коррелированные.
Теор. Если составлять двумерное нормальное распределение СВ Х и У некоррелированным, то СВ независимые.
Зам. Не всегда из некоррелированности => их независимость.(приводится пример почему это не так)
24.Теорема об условных распределениях компанент двумерной нормально распределенной св.
Теор. Если СВ (Х,У) распределена нормально с параметрами mх mу δх δу ρ, то условные распределения являются нормальными с параметрами:
для условного распределения составляет Х при фиксированном значении У=у и
mх/y= ρ(δх / δу)( у - mу)+ mх
δх/y = δх(1- ρ2)0.5
для условия распределения составн У при фиксированном значении Х=х
mу/х= ρ(δу / δх)( у – mх)+ mу
δу/х = δу(1- ρ2)0.5
Опр. Уравнение М(Х| У=у)= ρ(δх / δу)( у - mу)+ mх модельное уравнение регрессии Х и У аналогично М(У| Х=х)
Линии регрессии Х на У и У на Х в случае нормальнейшегося распределения – являются прямыми линиями , проходящими через точку с координатами (mх ,mу) – центр распределения двумерной СВ.
График условной плотности СВ У при условии что Х = х

25 Характеристические функции случайных величин, их свойства. Примеры
26. Неравенства Маркова и Чебышева.
Теорема(неравенство
Маркова):Пусть
собственная величина(СВ) Х принимает
только неотрицательные значения, тогда
![]() справедливы неравенства
справедливы неравенства ![]() .
.
Доказательство:
Докажем
для непрерывной СВ Х ![]() ,
,
![]() .
.

 ;
;
 ;
;
 .
доказано.
.
доказано.
Теорема(неравенство
Чебышева): Пусть
Х-СВ с дисперсией D(X),
тогда
справедливо неравенство  .
.
Доказательство:
Рассмотрим СВ ![]() ,
,
![]() ,
тогда для
,
тогда для ![]() справедливо неравенство Маркова
справедливо неравенство Маркова  ;
;
![]() ;
;
![]() из последних 2-х неравенств следует
неравенство. доказано.
из последних 2-х неравенств следует
неравенство. доказано.
27. Теорема Чебышева. Теорема Маркова.
Теорема
Чебышева: Пусть
![]() -
независимые СВ с конечными мат. ожиданиями
-
независимые СВ с конечными мат. ожиданиями
![]() ,
причем
,
причем ![]() ,
,
![]() тогда
тогда


Опр.
![]() по вероятности, если
по вероятности, если ![]() .
.
Доказательство:
Рассмотрим СВ  .
Найдем мат. ожидание и дисперсию:
.
Найдем мат. ожидание и дисперсию:  ;
;
 .
Применим неравенство Чебышева:
.
Применим неравенство Чебышева:  ;
;
 .
Пусть
.
Пусть ![]() и получаем утверждение теоремы.
и получаем утверждение теоремы.
Теорема
Маркова: Если
имеются зависимые СВ
и если при
выполняется  ,
то среднее арифметическое
,
то среднее арифметическое  сходится
по вероятности к среднему арифметическому
математических ожиданий
сходится
по вероятности к среднему арифметическому
математических ожиданий

Доказательство:
Аналогично
доказательству Чебышева 
 ;
;
 ;
;  ;
;
 .
доказано.
.
доказано.
28. Центральная предельная теорема.
Опр:
Пусть ![]() -
СВ. Случ. величину
-
СВ. Случ. величину 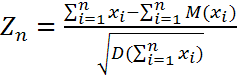 – нормированная сумма. Если
-независимые
СВ, то
– нормированная сумма. Если
-независимые
СВ, то  .
если
.
если ![]() ,
,
![]() -
одинаково распределены, то
-
одинаково распределены, то 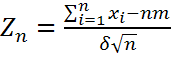 .
.
Теорема:
Если
![]() -
независимые СВ , имеющие один и той же
закон распределения с мат. ожидания
-
независимые СВ , имеющие один и той же
закон распределения с мат. ожидания
![]() ,
,
![]() ,
то
,
то 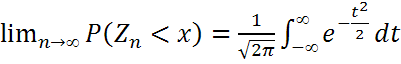 .
.
![]() -
распределена асимметрически при
по стандартному норм. закону.
-
распределена асимметрически при
по стандартному норм. закону.  .
.
Доказательство:
![]() ,
,
 ;
;
 ;
;
 ;
;
 ;
;
![]() ;
;
 ;
;
 .
.
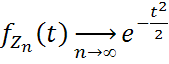 -
хар-ая функция стандартного нормального
закона распределения. Последовательность
функций распределения СВ
сходится к функции распределения
стандартного нормального закона
распределения. Это равносильно утверждению
теоремы. доказано.
-
хар-ая функция стандартного нормального
закона распределения. Последовательность
функций распределения СВ
сходится к функции распределения
стандартного нормального закона
распределения. Это равносильно утверждению
теоремы. доказано.
