16 Двумерные св. Условные законы распределения.

Опр: пусть (Х,У) дискретная двумерная СВ. Условным законом распределения случайной компоненты Х при условии, что компонента У приняла определенное значение называется совокупность возможных значений компоненты Х и соответств этим значениям условных вероятн

Аналогично определяется условный закон распределения случайной компоненты У при условии, что Х приняло определенное значение .

.

Опр: пусть (Х,У) – непрерывная 2-мерная СВ. Условной плотностью компоненты Х, при условии, что компонента У приняла определенное значение у, называется неотрицательная ф-ция действительной переменной х определенной при всех следующ формулой:

, где - одномерная плотн распр одномерн СВ

Аналогично определяется условная плотность .

Если известна плотность совместного распределения, то условные плотности компонент находятся по следующим формулам:

Условная плотность обладает св-вами:

17 Независимые случайные величины. Критерий независимости.

Опр: СВ называются независимыми, если закон распределения любого числа из них не зависит от того, какие возможные значения приняли остальные величины.

Равносильное опр: СВ называются независимыми (совокупностями), если для любого набора событий { }(i=1,2,3…n) где произвольные подмножества числовой оси, выполняется равенство: .

Для дискретной СВ равносильное определение: дискретные случайные величины называются независимыми, если для любых значений случайного вектора ( ) выполняется равенство:

Для непрерывных СВ :

Непрерывные СВ называются независимыми, если интервалов числовой оси выполняется равенство:

Теорема 1: случайные величины независимы т.т.т., когда в любой точке ( ) имеет место равенство:

Теорема 1: непрерывные СВ независимы когда выполняется равенство:

Док-во: Х, У -независимые СВ

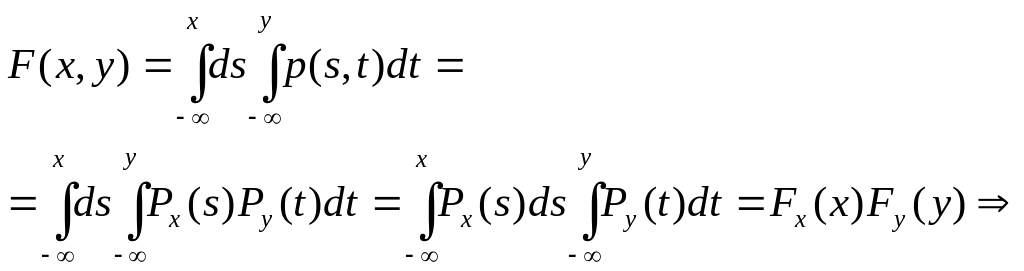по теореме 1 события Х и У независимые. 

Для дискретной СВ:

Для непрерывн СВ Х,У:

18 Функции случайных величин, их законы распределения.

Опр: пусть дана ф-ция одной переменной с областью определения D(f), и пусть дана некоторая СВ Х все значения которой принадлежат D(f). Тогда, если Х приняла значение х, будем считать, что новая СВ У приняла значение f(x). Эта новая СВ называется ф-цией СВ Х. В этом случае записываем: Y=f(X).

I. Выясним как найти распределение ф-ции одной СВ по известному распределению дискретного аргумента.

а) если различным возможным значениям аргумента Х соответствуют различные возможные значения ф-ции У, то вероятности соответствующих значений Х и У между собой равны:

б) если различным возможным значениям Х соотв значения У, среди которых есть равные между собой, то следует складывать вероятности повторяющихся вероятностей:

II. Та же задача ставится и для непрерывного аргумента: имеется плотность распределения СВ – р(х), а через нее хотим выразить .

Теорема: если f(x) дифференцируемая строго возрастающая ил строго убывающая ф-ция, обратная ф-ция которой , то имеет место равенство

Док-во: пусть и пусть множество значений СВ А это отрезок [a,b].

Ф-ция распределения СВ Y=f(X) имеет вид

f(x) - возрастает возрастает 

Замечание: можно рассматривать также ф-ции от 2 и более случайных величин