
- •1.Основные понятия теории вероятностей. Классическое, статистическое и геометрическое определения вероятности. Основные понятия тв.
- •Статистическое определение вероятности
- •Геометрическое определение вероятности
- •2. Алгебраические операции над событиями. Отношение м/д событиями. Аксиоматическое определение вероятности события. Отношение м/д событиями
- •Аксиоматическое определение вероятностей события
- •3.Основные свойства вероятностей. Правило сложения вероятностей. Условные вероятности. Теорема умножения вероятностей. Независимые события.
- •4.Формула полной вероятности. Формула Байеса.
- •5.Повторение испытаний. Формула Бернулли.
- •6.Локальная и интегральная теоремы Лапласа.
- •7. Вероятность отклонения относительной частоты от постоянной вероятности в независимых испытаниях.
- •8. Наивероятнейшее число появлений события при повторных испытаниях по схеме Бернулли.
- •9. Случайные величины. Закон распределения вероятностей. Биноминальное распределение. Геометрическое распределение.
- •10. Распределение Пуассона.
- •11. Функция распределения св и ее свойства.
- •12. Непрерывные св. Равномерный закон распределения.
- •13 Показательный закон распределения. Нормальный закон распределения.
- •14 Многомерные случайные величины. Ф-ция распределения многомерной случайной величины, её свойства.
- •15 Двумерные непрерывные св. Плотность распределения вероятностей двумерной св, её свойства
- •16 Двумерные св. Условные законы распределения.
- •17 Независимые случайные величины. Критерий независимости.
- •18 Функции случайных величин, их законы распределения.
- •19.Числовые характеритики св.
- •20.Моменты распределения одномерной св.
- •21.Ковариация и коэффициент линейной корреляции 2 св, их свойства.
- •22.Условное мат ожидание
- •23. Двумерное нормальное распределение. Условие независимости некоррелированных св.
- •24.Теорема об условных распределениях компанент двумерной нормально распределенной св.
- •25 Характеристические функции случайных величин, их свойства. Примеры
- •26. Неравенства Маркова и Чебышева.
- •27. Теорема Чебышева. Теорема Маркова.
- •28. Центральная предельная теорема.
- •29. Теорема Ляпунова. Интегральная теорема Лапласса.
- •30. Распределение выборки. Эмпирическая функция распределения.
- •33. Оценка дисперсии случайной величины.
- •34. Неравенство Рао-Крамера. Следствие для несмещенной оценки
- •35. Эффективная оценка мат. Ожидания нормальной распределенной величины.
- •36. Асимптотически эффективные и сверх эффективные оценки. Теорема о состоятельности оценки.
- •37. Условные законы распределения. Условное мат. Ожидание.
- •38.Достаточные статистики. Критерий факторизации
- •39.Теорема Колмагорова – Блекуэлла.
- •41. Метод моментов
- •42. Распределение….
- •43. Распределение Стьюдента.
- •44. Теоремы о случайной величине, имеющей распределение Стьюдента.
- •45. Распределение Фишера. Теорема о случайной величине, имеющей распределение Фишера
- •46 Доверительный интервал для мат. Ожидания нормально распределенной с.В.( -неизвестно)
- •47 Доверительный интервал для мат. Ожидания нормально распределенной с.В.( -известно)
- •48 Доверительный интервал для дисперсии нормально распределеннной с.В.
- •55 Проверка гипотезы о равенстве двух дисперсий нормально распределенный с.В.
33. Оценка дисперсии случайной величины.
![]()
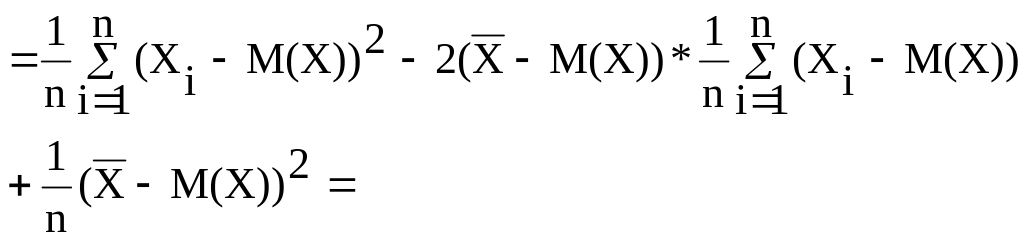
![]()
![]()
![]()
![]()
Док-жем,
что
![]() -состоятельн. оценка дисперсий случ.
величины х.
-состоятельн. оценка дисперсий случ.
величины х.

Рассм.
I:это
есть среднее арифметическое n
независимых одинаково распределенных
СВ
![]() согласно з-ну больших чисел (следствие
т.Чебышева) при
согласно з-ну больших чисел (следствие
т.Чебышева) при
![]() имеем:
имеем:
![]() (1)
(1)
Рассм.
II:
также в силу закона больших чисел.
![]() ,
поэтому
,
поэтому
![]() (2)
(2)
Из
выше сказанного следует, что
![]() .
Т.о.
.
Т.о.
![]() -состоятельная
оценка(хотя и смещенная).
-состоятельная
оценка(хотя и смещенная).
34. Неравенство Рао-Крамера. Следствие для несмещенной оценки
35. Эффективная оценка мат. Ожидания нормальной распределенной величины.
Опр.Несмещен.
Оценка ![]() пар-ра
пар-ра
![]() ,
для которой в нер-ве Рао-Крамера
достигается знак равенства,т.е.
,
для которой в нер-ве Рао-Крамера
достигается знак равенства,т.е.
 наз.
эффективной.
наз.
эффективной.
Пусть
Х случайная величина, имеющая нормальный
закон распределения с параметрами
![]() и
и
![]() .
.

Пусть
выборка (![]() явл. реализацией случайного вектора
явл. реализацией случайного вектора
![]() ,
где случайные величины
,
где случайные величины
![]() независимы
и распределены так же как и случайные
величины Х.
независимы
и распределены так же как и случайные
величины Х.
![]()
![]()
Покажем,
что
![]() -эффективная
оценка параметра
,
т.е. имеем
-эффективная
оценка параметра
,
т.е. имеем
-считаем
известным, а
-
неизвестным. Вычислим информацию Фишера
![]() .
.
![]()
![]()
![]()

![]()
![]()
![]()
![]()
36. Асимптотически эффективные и сверх эффективные оценки. Теорема о состоятельности оценки.
Определение:
несмещенная оценка ![]() называется асимптотически эффективной
оценкой параметра
называется асимптотически эффективной
оценкой параметра
![]() ,
если
,
если
![]() D(
D(![]() )*Jn(
)*Jn(![]() )=1
)=1
D( )=1/ Jn(ϴ)
Определение : Если условия дифференцирования интегралов по параметру при котором доказывается неравенства Рао-Крамера не выполняется, то может существовать несмещенная оценка дисперсия которой меньше чем нижняя граница в неравенстве Рао-Крамера. Такая оценка называется сверхэффективной.
= (X1, ... , Xn)
Если
M( )
)![]() ,
а D(
,
а D(![]() )
при n
)
при n![]() ,
то
-
является состоятельной.
,
то
-
является состоятельной.
Д-во :
В
силу неравенства Чебышева (*):
![]()
![]()
значит
и p
.
![]() .
Обозначим
.
Обозначим
![]() =
=![]()
В
силу условия ![]() при
при
![]() :
:
![]()
![]()
![]()
![]() >2*
>2*![]()
Возьмем
n-настолько
большое, чтобы выполнялось это неравенство:
2*
>![]() ,
так как
,
так как
![]()
Тогда
![]() >
}
>
}
В
силу (*) получаем, что
при
![]() .
Значит
.
Значит
![]() -
состоятельная оценка.
-
состоятельная оценка.
Ч.т.д.
37. Условные законы распределения. Условное мат. Ожидание.
Дискретное
распределения. Рассм.
случ. метод
![]() =(X1,
... , Xn),
где Xi
–
случ. вел. Пусть
– имеет дискр. распр.:
P{
=X}=p(x)=p(x1,
... , xn).
x-
пробегает конечное или счетное множество
возможных значений
.
По свойствам этих вероятностей: p(x)
=(X1,
... , Xn),
где Xi
–
случ. вел. Пусть
– имеет дискр. распр.:
P{
=X}=p(x)=p(x1,
... , xn).
x-
пробегает конечное или счетное множество
возможных значений
.
По свойствам этих вероятностей: p(x)![]() .
Рассмотрим функцию : t=t(x1,
... , xn).
В дальнейшем вместо функции t(x1,
... , xn)
можно рассматривать вектор функцию
t(x).
Определение:Условным
распределением
при
условий t(
)=t
(t-фиксир)
назовем совокупность условных вероятностей
P(x|t)=P{
=X|t(
)=t}.
.
Рассмотрим функцию : t=t(x1,
... , xn).
В дальнейшем вместо функции t(x1,
... , xn)
можно рассматривать вектор функцию
t(x).
Определение:Условным
распределением
при
условий t(
)=t
(t-фиксир)
назовем совокупность условных вероятностей
P(x|t)=P{
=X|t(
)=t}.
Если
x
и t
таковы, что t(x)![]() t,
то очевидно, что p(x|t))=0
t,
то очевидно, что p(x|t))=0
Замечание : В дальнейшем считаем, что t(x)=t
Выразим
усл. вер. p(x|t),
через вероятность p(x).P{
=X|t(
)=t}=
![]()
![]() (*)
(*)
Доп.
усл. на t:
t
– выбирается таким, чтобы знаменатель
последней дроби не был равен нулю,
другими словами, чтобы на линии уров-ня
было хотя бы одно
с
ненулевой вероятностью.Пусть g(x)
– числовая функция от векторного
аргумента x=(x1,
... , xn),
тогда g(
)
– случ. величина, ее мат ожидание:
M[g(
)]=![]()
Условное мат. ожидание случайной величины g( ), при t( )=t определяется с помощью условного распределения.
Определение.Условное
мат ожидание случайной величины g(X)
при условии t(
)=t
обозначим M[g(
)|t(
)=t]=
![]() .
В силу (*) имеем :
.
В силу (*) имеем :
M[g(
)|t(
)=t]= .
.
Условное
мат. ожидание : M{g(
)|t(
)=t}
– обозначение ее g1(t).
Вместо t
в эту функцию подставим случ. величину
![]() t(
),
мы получим, что усл мат ожидание есть
случайная величина g1(
t(
),
мы получим, что усл мат ожидание есть
случайная величина g1(![]() )
)
M[g1(
)]=![]()

![]() =
=![]()
Т.о. мы доказали: M[g( )]=M[M(g( )|t)] (****)
Т. е. при вычислении мат. ожидания случ. величины g( )сначало можно вычислить условное мат. ожидание g( ), при условии t( )=t , а затем осреднить это усл. мат. ожидание по вероятностям условий.
Непрерывное распределение. Пусть - имеет непрерывное распределение и t(x)=t(x1, ... , xn) – некоторые функции от n-переменных.
Определение
:
предел при
![]() след. величины:
след. величины:
![]() назыв.
усл. плотностью случайного вектора
при условии t(
)=t
и обозн. p(x|t).
Пусть g(x)
– некоторая функция (x1,
... ,xn).
Усл. мат ожидание случ величины g(
)
при условии t(
)=t
определяется: M{g(
)|t(
)=t}=
назыв.
усл. плотностью случайного вектора
при условии t(
)=t
и обозн. p(x|t).
Пусть g(x)
– некоторая функция (x1,
... ,xn).
Усл. мат ожидание случ величины g(
)
при условии t(
)=t
определяется: M{g(
)|t(
)=t}=![]() .
Формула (***) имеет место и в случае, если
имеет
непрерывное распределение.
.
Формула (***) имеет место и в случае, если
имеет
непрерывное распределение.
