
- •1.Основные понятия теории вероятностей. Классическое, статистическое и геометрическое определения вероятности. Основные понятия тв.
- •Статистическое определение вероятности
- •Геометрическое определение вероятности
- •2. Алгебраические операции над событиями. Отношение м/д событиями. Аксиоматическое определение вероятности события. Отношение м/д событиями
- •Аксиоматическое определение вероятностей события
- •3.Основные свойства вероятностей. Правило сложения вероятностей. Условные вероятности. Теорема умножения вероятностей. Независимые события.
- •4.Формула полной вероятности. Формула Байеса.
- •5.Повторение испытаний. Формула Бернулли.
- •6.Локальная и интегральная теоремы Лапласа.
- •7. Вероятность отклонения относительной частоты от постоянной вероятности в независимых испытаниях.
- •8. Наивероятнейшее число появлений события при повторных испытаниях по схеме Бернулли.
- •9. Случайные величины. Закон распределения вероятностей. Биноминальное распределение. Геометрическое распределение.
- •10. Распределение Пуассона.
- •11. Функция распределения св и ее свойства.
- •12. Непрерывные св. Равномерный закон распределения.
- •13 Показательный закон распределения. Нормальный закон распределения.
- •14 Многомерные случайные величины. Ф-ция распределения многомерной случайной величины, её свойства.
- •15 Двумерные непрерывные св. Плотность распределения вероятностей двумерной св, её свойства
- •16 Двумерные св. Условные законы распределения.
- •17 Независимые случайные величины. Критерий независимости.
- •18 Функции случайных величин, их законы распределения.
- •19.Числовые характеритики св.
- •20.Моменты распределения одномерной св.
- •21.Ковариация и коэффициент линейной корреляции 2 св, их свойства.
- •22.Условное мат ожидание
- •23. Двумерное нормальное распределение. Условие независимости некоррелированных св.
- •24.Теорема об условных распределениях компанент двумерной нормально распределенной св.
- •25 Характеристические функции случайных величин, их свойства. Примеры
- •26. Неравенства Маркова и Чебышева.
- •27. Теорема Чебышева. Теорема Маркова.
- •28. Центральная предельная теорема.
- •29. Теорема Ляпунова. Интегральная теорема Лапласса.
- •30. Распределение выборки. Эмпирическая функция распределения.
- •33. Оценка дисперсии случайной величины.
- •34. Неравенство Рао-Крамера. Следствие для несмещенной оценки
- •35. Эффективная оценка мат. Ожидания нормальной распределенной величины.
- •36. Асимптотически эффективные и сверх эффективные оценки. Теорема о состоятельности оценки.
- •37. Условные законы распределения. Условное мат. Ожидание.
- •38.Достаточные статистики. Критерий факторизации
- •39.Теорема Колмагорова – Блекуэлла.
- •41. Метод моментов
- •42. Распределение….
- •43. Распределение Стьюдента.
- •44. Теоремы о случайной величине, имеющей распределение Стьюдента.
- •45. Распределение Фишера. Теорема о случайной величине, имеющей распределение Фишера
- •46 Доверительный интервал для мат. Ожидания нормально распределенной с.В.( -неизвестно)
- •47 Доверительный интервал для мат. Ожидания нормально распределенной с.В.( -известно)
- •48 Доверительный интервал для дисперсии нормально распределеннной с.В.
- •55 Проверка гипотезы о равенстве двух дисперсий нормально распределенный с.В.
1.Основные понятия теории вероятностей. Классическое, статистическое и геометрическое определения вероятности. Основные понятия тв.
Под событием ТВ понимается всякий факт, который в результате опыта может произойти или не произойти.
Примеры: А-появление герба при бросании монеты; В-появление 3-х гербов при 3-х кратном бросании монеты; С-попадание в цель при выстреле.
Будем
рассматривать вначале классическую
вероятностную модель, которая используется
для описания опытов с конечным числом
взаимно-исключающих возможных исходов.
Пусть результаты опыта описываются с
взаимно-исключающими исходами ![]() .
Эти исходы называют также элементарными
событиями.
Мн-во
.
Эти исходы называют также элементарными
событиями.
Мн-во ![]() –это мн-во всех элементарных исходов
называют множеством элементарных
событий. Любое случайное событие А
связанное с данным опытом может быть
связано посредством перечисления всех
элементарных событий, при которых оно
происходит A={
–это мн-во всех элементарных исходов
называют множеством элементарных
событий. Любое случайное событие А
связанное с данным опытом может быть
связано посредством перечисления всех
элементарных событий, при которых оно
происходит A={![]() }.
Исходы
наз-ют благоприятствующими
событию А.
Событие
}.
Исходы
наз-ют благоприятствующими
событию А.
Событие ![]() состоящее из всех возможных исходов
наз-ют достоверным.
|A|-число
элементарных событий входящих в А.
Вероятность
-
числовая характеристика степени
возможности появления какого-либо
определённого события в тех или иных
определимых могущих повторятся
неограниченное число раз (обозначение
P(A)).
состоящее из всех возможных исходов
наз-ют достоверным.
|A|-число
элементарных событий входящих в А.
Вероятность
-
числовая характеристика степени
возможности появления какого-либо
определённого события в тех или иных
определимых могущих повторятся
неограниченное число раз (обозначение
P(A)).
Классическое
определение вероятности:Классические
вероятностные модели P(A)=![]() (*). Более общий подход в определении
P(A)
следующий: с каждым из элементарных
исходов связывающие неотрицательное
число
(*). Более общий подход в определении
P(A)
следующий: с каждым из элементарных
исходов связывающие неотрицательное
число ![]() причём
причём ![]() .
Пусть A={
}
тогда полагают, что P(A)=
.
Пусть A={
}
тогда полагают, что P(A)=![]() .
Легко видеть, что (*) получается из
послед-ей в случае, если
.
Легко видеть, что (*) получается из
послед-ей в случае, если 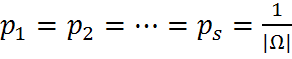 .
.
 ,
, ![]()
![]()
![]() число перестановок из m
элементов
число перестановок из m
элементов
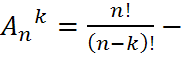 число
упорядоченных размещений из n
элементов по k
число
упорядоченных размещений из n
элементов по k
Статистическое определение вероятности
В
основе лежит эксперимент. Проводят
серию из n
опытов, в каждом из которых может
появиться событие A.Пусть
А появилось в m
случаях, тогда величина ![]() наз-ся относительной
частотой события
А. Её часто наз-ют статистической
вероятностью события А. Обозначение:
наз-ся относительной
частотой события
А. Её часто наз-ют статистической
вероятностью события А. Обозначение:
![]() .
.

Геометрическое определение вероятности
Геометрической
вероятностью явл-ся вероятностной
моделью с бесконечным числом исходов.
Возьмём в качестве элементарных событий
мн-во точек плоскости. Считаем, что в
этой плоскости задана система ккординат,
Ω![]() событие A
событие A![]() .
Вероятностью события А в модели геом-х
вероятностей наз-ся число P(A)=
.
Вероятностью события А в модели геом-х
вероятностей наз-ся число P(A)=
2. Алгебраические операции над событиями. Отношение м/д событиями. Аксиоматическое определение вероятности события. Отношение м/д событиями
А\В-это событие состоящее в том, что А происходит, а В-нет.
Свойства алгебраических операций над событиями:
А+В=В+А
А*В=В*А
(А+В)+С=А+(В+С)
(А*В)*С=А*(В*С)
(А+В)*С=А*С+В*С
А
и В события, А![]() В-событие
А влечёт за собой событие В.
В-событие
А влечёт за собой событие В.

А=В- событие А тождественно событию В и означает А В и В А.
Система F подмножеств множества такая, что:
Ω

если А, В , то А+В и А*В
если А , то

называется
алгеброй.
Система
F
замкнута относительно операций
+,*,![]() -отрицание.
Если система F
замкнута относительно алгебраических
операций над счётным числом событий,
то она наз-ся σ-алгеброй.(
-отрицание.
Если система F
замкнута относительно алгебраических
операций над счётным числом событий,
то она наз-ся σ-алгеброй.(![]() )
)
Счётное мн-во - бесконечное мн-во м/д элементами, которого и элементами мн-ва натуральных чисел можно установить взаимно однозначное соответствие.
