24.2. Геометрический смысл дифференциала функции

Выясним геометрический смысл дифференциала.

Для этого проведем к графику функции у=ƒ(х) в точке М(х; у) касательную МТ и рассмотрим ординату этой касательной для точки х+∆х (см. рис. 138). На рисунке ½ АМ½ =∆х, |AM₁|=∆у. Из прямоугольного треугольника МАВ имеем:

Но, согласно геометрическому смыслу производной, tga=ƒ'(х). Поэтому АВ=ƒ'(х)•∆х.

Сравнивая полученный результат с формулой (24.1), получаем dy=АВ, т. е. дифференциал функции у=ƒ(х) в точке х равен приращению ординаты касательной к графику функции в этой точке, когда х получит приращение ∆х.

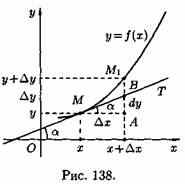
В этом и состоит геометрический смысл дифференциала.

24.3 Основные теоремы о дифференциалах

Основные теоремы о дифференциалах легко получить, используя связь дифференциала и производной функции (dy=f'(x)dx) и соответствующие теоремы о производных.

Например, так как производная функции у=с равна нулю, то дифференциал постоянной величины равен нулю: dy=с'dx=0•dx=0.

Теорема 24.1. Дифференциал суммы, произведения и частного двух дифференцируемых функций определяются следующими формулами:

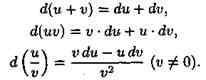
Докажем, например, вторую формулу. По определению дифференциала имеем:

d(uv)=(uv)'dx=(uv'+vu')dx=vu'dx+uv'dx=udv+vdu

Теорема 24.2. Дифференциал сложной функции равен произведению производной этой функции по промежуточному аргументу на дифференциал этого промежуточного аргумента.

Пусть у=ƒ(u) и u=φ(х) две дифференцируемые функции, образующие сложную функцию у=ƒ(φ(х)). По теореме о производной сложной функции можно написать

у'_х=у'_u•u'_x.

Умножив обе части этого равенства на dx, поучаем у'_хdx=у'_u•u'_хdx. Но у'_хdx=dy и u'_хdx=du. Следовательно, последнее равенство можно переписать так:

dy=у'_udu.

Сравнивая формулы dy=у'_х•dx и dy=у'_u•du, видим, что первый дифференциал функции у=ƒ(х) определяется одной и той же формулой независимо от того, является ли ее аргумент независимой переменной или является функцией другого аргумента.

Это свойство дифференциала называют инвариантностью (неизменностью) формы первого дифференциала.

Формула dy=у'_х•dx по внешнему виду совпадает с формулой dy=у'_u•du, но между ними есть принципиальное отличие: в первой формуле х — независимая переменная, следовательно, dx=∆х, во второй формуле и есть функция от х, поэтому, вообще говоря, du≠∆u.

С помощью определения дифференциала и основных теорем о дифференциалах легко преобразовать таблицу производных в таблицу дифференциалов.

Например: d(cosu)=(cosu)'_udu=-sinu•du

24.4. Таблица дифференциалов

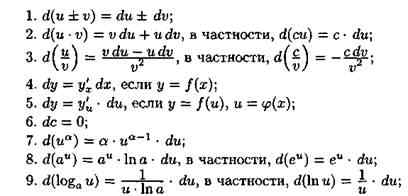
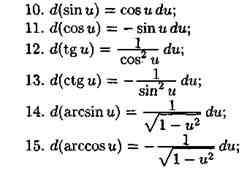
24.5. Применение дифференциала к приближенным вычислениям

Как уже известно, приращение ∆у функции у=ƒ(х) в точке х можно представить в виде ∆у=ƒ'(х)•∆х+α•∆х, где α→0 при ∆х→0, или ∆у=dy+α•∆х. Отбрасывая бесконечно малую α•∆х более высокого порядка, чем ∆х, получаем приближенное равенство

∆у≈dy,                                              (24.3)

причем это равенство тем точнее, чем меньше ∆х.

Это равенство позволяет с большой точностью вычислить приближенно приращение любой дифференцируемой функции.

Дифференциал обычно находится значительно проще, чем приращение функции, поэтому формула (24.3) широко применяется в вычислительной практике.

<< Пример 24.3

Найти приближенное значение приращения функции у=х³-2х+1 при х=2 и ∆х=0,001.

Решение: Применяем формулу (24.3): ∆у≈dy=(х³-2х+1)'•∆х=(3х²-2)•∆х.

Итак, ∆у» 0,01.

Посмотрим, какую погрешность допустили, вычислив дифференциал функции вместо ее приращения. Для этого найдем ∆у:

∆у=((х+∆х)³-2(х+∆х)+1)-(х³-2х+1)=х³+3х²•∆х+3х•(∆х)²+(∆х)³-2х-2•∆х+1-х³+2х-1=∆х(3х²+3х•∆х+(∆х)²-2);

Абсолютная погрешность приближения равна

|∆у-dy|=|0,010006-0,011=0,000006.

Подставляя в равенство (24.3) значения ∆у и dy, получим

ƒ(х+∆х)-ƒ(х)≈ƒ'(х)∆х

или

ƒ(х+∆х)≈ƒ(х)+ƒ'(х)•∆х.                            (24.4)

Формула (24.4) используется для вычислений приближенных значений функций.

<< Пример 24.4

Вычислить приближенно arctg(1,05).

Решение: Рассмотрим функцию ƒ(х)=arctgx. По формуле (24.4) имеем:

arctg(x+∆х)≈arctgx+(arctgx)'•∆х,

т. е.

Так как х+∆х=1,05, то при х=1 и ∆х=0,05 получаем:

Можно показать, что абсолютная погрешность формулы (24.4) не превышает величины М•(∆х)², где М — наибольшее значение |ƒ"(х)| на сегменте [х;х+∆х].

<< Пример 24.5

Какой путь пройдет тело при свободном падении на Луне за 10,04 с от начала падения. Уравнение свободного падения тела

H=g_лt²/2, g_л=1,6 м/с².

Какой путь пройдет тело при свободном падении на Луне за 10,04 с от начала падения. Уравнение свободного падения тела

H=g_лt²/2, g_л=1,6 м/с².

Решение: Требуется  найти  H(10,04).   Воспользуемся  приближенной формулой (ΔH≈dH)

H(t+∆t)≈H(t)+H'(t)•∆t. При t=10 с и ∆t=dt=0,04 с, H'(t)=g_лt, находим

Задача (для самостоятельного решения). Тело массой m=20 кг движется со скоростью ν=10,02 м/с. Вычислить приближенно кинетическую энергию тела