
- •13. Множества. Действительные числа
- •13.1 Основные понятия
- •13.2. Числовые множества. Множество действительных чисел
- •13.3 Числовые промежутки. Окрестность точки
- •§ 14. Функция
- •14.1. Понятие функции.
- •14.2 Числовые функции. График функции. Способы задания функций
- •14.3. Основные характеристики функции
- •14.4. Обратная функция
- •14.5 Сложная функция
- •14.6 Основные элементарные функции и их графики
- •§ 15. Последовательности
- •15. Последовательности
- •15.1 Числовая последовательность
- •15.2. Предел числовой последовательности
- •15.4. Предел монотонной ограниченной последовательности. Число е. Натуральные логарифмы
- •§ 16. Предел функции
- •16. Предел функции
- •16.1. Предел функции в точке
- •16.2. Односторонние пределы
- •16.3. Предел функции при х ® ∞
- •16.4. Бесконечно большая функция (б.Б.Ф.)
- •§ 17. Бесконечно малые функции (б.М.Ф.)
- •17. Бесконечно малые функции (б.М.Ф.)
- •17.1. Определения и основные теоремы
- •17.2. Связь между функцией, ее пределом и бесконечно малой функцией
- •17.3. Основные теоремы о пределах
- •17.4. Признаки существования пределов
- •17.5. Первый замечательный предел
- •17.6. Второй замечательный предел
- •§ 18. Эквивалентные бесконечно малые функции
- •18. Эквивалентные бесконечно малые функции
- •18.1. Сравнение бесконечно малых функций
- •18.2. Эквивалентные бесконечно малые и основные теоремы о них
- •18.3. Применение эквивалентных бесконечно малых функций
- •18.4 Приближенные вычисления
- •§ 19. Непрерывность функций
- •19. Непрерывность функций
- •19.1. Непрерывность функции в точке
- •19.2. Непрерывность функции в интервале и на отрезке
- •19.3. Точки разрыва функции и их классификация
- •19.4. Основные теоремы о непрерывных функциях.
- •19.5. Свойства функций, непрерывных на отрезке
- •§ 20. Производная функции
- •20. Производная функции
- •20.1. Задачи, приводящие к понятию производной
- •20.2. Определение производной; ее механический и геометрический смысл.
- •20.3. Связь между непрерывностью и дифференцируемостью функции
- •20.4. Производная суммы, разности, произведения и частного функций
- •20.5. Производная сложной и обратной функций
- •20.6. Производные основных элементарных функций
- •20.7. Гиперболические функции и их производные
- •20.8. Таблица производных
- •§ 21. Дифференцирование неявных и параметрически заданных функций
- •21. Дифференцирование неявных и параметрически заданных функций
- •21.1. Неявно заданная функция
- •21.2. Функция, заданная параметрически
- •22. Логарифмическое дифференцирование
- •§23. Производные высших порядков
- •23. Производные высших порядков
- •23.1. Производные высших порядков явно заданной функции
- •23.2. Механический смысл производной второго порядка
- •23.3. Производные высших порядков неявно заданной функции
- •23.4. Производные высших порядков от функций, заданных параметрически
- •§24. Дифференциал функции
- •24. Дифференциал функции
- •24.1. Понятие дифференциала функции
- •24.2. Геометрический смысл дифференциала функции
- •24.3 Основные теоремы о дифференциалах
- •24.4. Таблица дифференциалов
- •24.5. Применение дифференциала к приближенным вычислениям
- •24.6. Дифференциалы высших порядков
- •§ 25. Исследование функций при помощи производных
- •25.1. Некоторые теоремы о дифференцируемых функциях
- •25.2. Правила Лопиталя
- •25.3. Возрастание и убывание функций
- •25.4. Максимум и минимум функций
- •25.5. Наибольшее и наименьшее значения функции на отрезке
- •25.6. Выпуклость графика функции. Точки перегиба
- •25.7. Асимптоты графика функции
- •25.8. Общая схема исследования функции и построения графика
- •§ 26. Формула Тейлора
- •26. Формула тейлора
- •26.1. Формула Тейлора для многочлена
- •26.2. Формула Тейлора для произвольной функции
21.2. Функция, заданная параметрически
Пусть зависимость между аргументом х и функцией у задана параметрически в виде двух уравнений
![]()
где t — вспомогательная переменная, называемая параметром.
Найдем производную у'х, считая, что функции (21.1) имеют производные и что функция х=x(t) имеет обратную t=φ(х). По правилу дифференцирования обратной функции
![]()
Функцию у=ƒ(х), определяемую параметрическими уравнениями (21.1), можно рассматривать как сложную функцию у=y(t), где t=φ(х). По правилу дифференцирования сложной функции имеем: у'х=y't•t'x. С учетом равенства (21.2) получаем
![]()
Полученная формула позволяет находить производную у'х от функции заданной параметрически, не находя непосредственной зависимости у от х.
<< Пример 21.2
Пусть ![]()
Найти у'х.
Решение:
Имеем x't=3t2,
y't=2t.
Следовательно, у'х=2t/t2,
т. е. ![]()
В этом можно убедиться, найдя непосредственно зависимость у от х.
Действительно, ![]() Тогда
Тогда ![]() Отсюда
Отсюда![]() т.
е.
т.
е.![]()
22. Логарифмическое дифференцирование
В ряде случаев для нахождения производной целесообразно заданную функцию сначала прологарифмировать. А затем результат продифференцировать. Такую операцию называют логарифмическим дифференцированием.
<< Пример 22.1
Найти
производную функции ![]()
Решение: Пользуясь формулой (22.1), получаем:
![]()
Отметим, что запоминать формулу (22.1) необязательно, легче запомнить суть логарифмического дифференцирования.
Существуют функции, производные которых находят лишь логарифмическим дифференцированием. К их числу относится так называемая степенно-показательная функция у=uv, где u=u(x) и ν=ν(х) - заданные дифференцируемые функции от х. Найдем производную этой функции:

Сформулируем правило запоминания формулы (22.1): производная степенно-показательной функции равна сумме производной показательной функции, при условии u=const, и производной степенной функции, при условии ν=const.
§23. Производные высших порядков
Додати до моєї бази знань |
Математика |
23. Производные высших порядков
23.1. Производные высших порядков явно заданной функции
Производная у'=ƒ'(х) функции у=ƒ(х) есть также функция от х и называется производной первого порядка.
Если
функция ƒ'(х) дифференцируема, то ее
производная называется производной
второго порядка и обозначается у"
![]()
![]()
Итак, у"=(у')'.
Производная от производной второго порядка, если она существует, называется производной третьего порядка и обозначается у'" (или ƒ'"(х)). Итак, у'"=(y")'
Производной n-го порядка (или n-й производной) называется производная от производной (n-1) порядка:
y(n)=(y(n-1))¢ .
Производные порядка выше первого называются производными высших порядков.
Начиная с производной четвертого порядка, производные обозначают римскими цифрами или числами в скобках (уν или у(5)— производная пятого порядка).
<< Пример 23.1
Найти производную 13-го порядка функции у=sinx.
Решение:
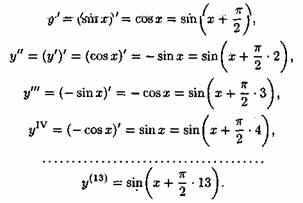
23.2. Механический смысл производной второго порядка
Пусть материальная точка М движется прямолинейно по закону S=f(t). Как уже известно, производная S¢ t равна скорости точки в данный момент времени: S't=V.
Покажем, что вторая производная от пути по времени есть величина, ускорения прямолинейного движения точки, т. е. S"=α.
Пусть в момент времени t скорость точки равна V, а в момент t+∆t — скорость равна V+∆V, т. е. за промежуток времени ∆t скорость изменилась на величину ∆V.
Отношение ∆V/∆t выражает среднее ускорение движения точки за время ∆t. Предел этого отношения при ∆t→0 называется ускорением точки М в данный момент t и обозначается буквой α:
![]()
Но V=S't. Поэтому α=(S't)', т. е. α=S't'
