
- •13. Множества. Действительные числа
- •13.1 Основные понятия
- •13.2. Числовые множества. Множество действительных чисел
- •13.3 Числовые промежутки. Окрестность точки
- •§ 14. Функция
- •14.1. Понятие функции.
- •14.2 Числовые функции. График функции. Способы задания функций
- •14.3. Основные характеристики функции
- •14.4. Обратная функция
- •14.5 Сложная функция
- •14.6 Основные элементарные функции и их графики
- •§ 15. Последовательности
- •15. Последовательности
- •15.1 Числовая последовательность
- •15.2. Предел числовой последовательности
- •15.4. Предел монотонной ограниченной последовательности. Число е. Натуральные логарифмы
- •§ 16. Предел функции
- •16. Предел функции
- •16.1. Предел функции в точке
- •16.2. Односторонние пределы
- •16.3. Предел функции при х ® ∞
- •16.4. Бесконечно большая функция (б.Б.Ф.)
- •§ 17. Бесконечно малые функции (б.М.Ф.)
- •17. Бесконечно малые функции (б.М.Ф.)
- •17.1. Определения и основные теоремы
- •17.2. Связь между функцией, ее пределом и бесконечно малой функцией
- •17.3. Основные теоремы о пределах
- •17.4. Признаки существования пределов
- •17.5. Первый замечательный предел
- •17.6. Второй замечательный предел
- •§ 18. Эквивалентные бесконечно малые функции
- •18. Эквивалентные бесконечно малые функции
- •18.1. Сравнение бесконечно малых функций
- •18.2. Эквивалентные бесконечно малые и основные теоремы о них
- •18.3. Применение эквивалентных бесконечно малых функций
- •18.4 Приближенные вычисления
- •§ 19. Непрерывность функций
- •19. Непрерывность функций
- •19.1. Непрерывность функции в точке
- •19.2. Непрерывность функции в интервале и на отрезке
- •19.3. Точки разрыва функции и их классификация
- •19.4. Основные теоремы о непрерывных функциях.
- •19.5. Свойства функций, непрерывных на отрезке
- •§ 20. Производная функции
- •20. Производная функции
- •20.1. Задачи, приводящие к понятию производной
- •20.2. Определение производной; ее механический и геометрический смысл.
- •20.3. Связь между непрерывностью и дифференцируемостью функции
- •20.4. Производная суммы, разности, произведения и частного функций
- •20.5. Производная сложной и обратной функций
- •20.6. Производные основных элементарных функций
- •20.7. Гиперболические функции и их производные
- •20.8. Таблица производных
- •§ 21. Дифференцирование неявных и параметрически заданных функций
- •21. Дифференцирование неявных и параметрически заданных функций
- •21.1. Неявно заданная функция
- •21.2. Функция, заданная параметрически
- •22. Логарифмическое дифференцирование
- •§23. Производные высших порядков
- •23. Производные высших порядков
- •23.1. Производные высших порядков явно заданной функции
- •23.2. Механический смысл производной второго порядка
- •23.3. Производные высших порядков неявно заданной функции
- •23.4. Производные высших порядков от функций, заданных параметрически
- •§24. Дифференциал функции
- •24. Дифференциал функции
- •24.1. Понятие дифференциала функции
- •24.2. Геометрический смысл дифференциала функции
- •24.3 Основные теоремы о дифференциалах
- •24.4. Таблица дифференциалов
- •24.5. Применение дифференциала к приближенным вычислениям
- •24.6. Дифференциалы высших порядков
- •§ 25. Исследование функций при помощи производных
- •25.1. Некоторые теоремы о дифференцируемых функциях
- •25.2. Правила Лопиталя
- •25.3. Возрастание и убывание функций
- •25.4. Максимум и минимум функций
- •25.5. Наибольшее и наименьшее значения функции на отрезке
- •25.6. Выпуклость графика функции. Точки перегиба
- •25.7. Асимптоты графика функции
- •25.8. Общая схема исследования функции и построения графика
- •§ 26. Формула Тейлора
- •26. Формула тейлора
- •26.1. Формула Тейлора для многочлена
- •26.2. Формула Тейлора для произвольной функции
20.7. Гиперболические функции и их производные
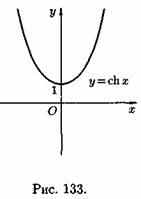
В математике, механике, электротехнике и некоторых других дисциплинах встречаются гиперболические функции, определяемые следующими формулами:
![]() —
гиперболический
синус;
—
гиперболический
синус;
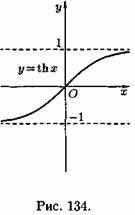
![]() —
гиперболический
косинус («цепная линия»);
—
гиперболический
косинус («цепная линия»);
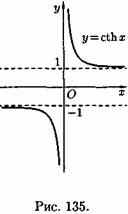
![]() —
гиперболический
тангенс и котангенс, где е — неперово
число.
—
гиперболический
тангенс и котангенс, где е — неперово
число.
На рисунках (132-135) показаны графики гиперболических функций.
Между гиперболическими функциями существуют следующие основные зависимости:
ch2x-sh2x=1;
sh(x ± у) = sh х • ch у ± ch x • sh у;
ch(x ± у) = ch x • ch у ± sh x • sh у;
![]()
sh 2x = 2 sh x • ch x; ch 2x = ch2 x + sh2 x.
Все эти формулы вытекают из определения гиперболических функций.
Например,
![]()
![]()
Геометрическая интерпретация гиперболических функций (см. рис. 137) аналогична интерпретации тригонометрических функций (см. рис. 136).
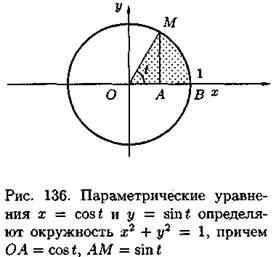
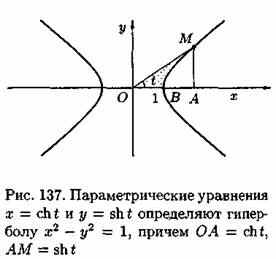
Найдем производные гиперболических функций:
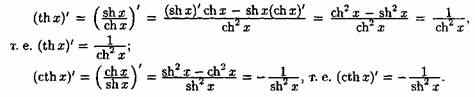
20.8. Таблица производных
Выведенные правила дифференцирования, формулы производных основных элементарных функций запишем в виде таблицы.
На практике чаще всего приходится находить производные от сложных функций. Поэтому в приведенной ниже таблице формул дифференцирования аргумент «х» заменен на промежуточный аргумент «u».
Правила дифференцирования
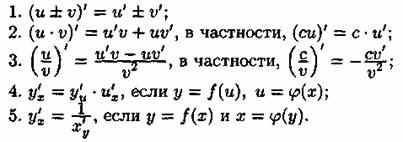
Формулы дифференцирования
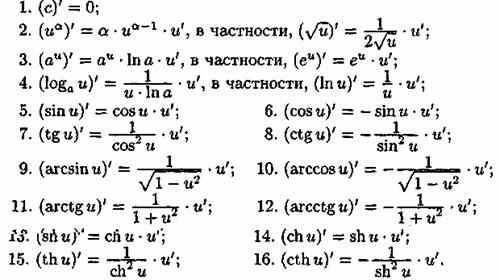
Для вычисления производных надо знать лишь правила дифференцирования и формулы производных основных элементарных функций, строго соблюдать эти правила при выполнении упражнений.
<< Пример 20.10
Найти производную функции у=х4-3х3+2х-1.
Решение: у'=(х4-3х3+2х-1)'=(х4)'-(3х3)'+(2х)'-(1)'=4х3-3(х3)' Надо стараться обходиться без лишних записей.
<< Пример 20.11
Найти производную функции у=2х3/tg х
Решение:
![]()
Производная найдена. В процессе решения использованы правила 2, 3 и формулы 2, 7.
<< Пример 20.12
Найти производную функции у=cos(ln122x).
Решение: Коротко: у'=-sin(ln122x)•12ln112x•1/2х•2.
Решение с пояснениями: данную функцию можно представить следующим образом: у=cos(u), u=t12, t=ln(z), z=2x. Производную сложной функции найдем по правилу у'х=у'u•u't•t'z•z'х (здесь промежуточных аргументов три):
у'х=-sinu•12•t11•1/z•2, у'х=-sint12•12•(lnz)11•1/2x•2, у'х=-sin(lnz)12•12•ln11z•1/x, у'х=-sin(ln122x)•12•ln112x•1/x, Окончательно у'х=-12•sin(ln122x)•ln112x•1/x
§ 21. Дифференцирование неявных и параметрически заданных функций
21. Дифференцирование неявных и параметрически заданных функций
21.1. Неявно заданная функция
Если функция задана уравнением у=ƒ(х), разрешенным относительно у, то функция задана в явном виде (явная функция).
Под неявным заданием функции понимают задание функции в виде уравнения F(x;y)=0, не разрешенного относительно у.
Всякую явно заданную функцию у=ƒ (х) можно записать как неявно заданную уравнением ƒ(х)-у=0, но не наоборот.
Не всегда легко, а иногда и невозможно разрешить уравнение относительно у (например, у+2х+cosy-1=0 или 2у-х+у=0).
Если неявная функция задана уравнением F(x; у)=0, то для нахождения производной от у по х нет необходимости разрешать уравнение относительно у: достаточно продифференцировать это уравнение по x, рассматривая при этом у как функцию х, и полученное затем уравнение разрешить относительно у'.
Производная неявной функции выражается через аргумент х и функцию у.
<< Пример 21.1
Найти производную функции у, заданную уравнением х3+у3-3ху=0.
Решение: Функция у задана неявно. Дифференцируем по х равенство х3+у3-3ху=0. Из полученного соотношения
3х2+3у2· у'-3(1· у+х· у')=0
следует, что у2у'-ху'=у-х2, т. е. у'=(у-х2)/(у2-х).
