Товарообіг і зміна фізичного обсягу продукції

	Продукти		Обсяг товарообігу в базисному періоді, грн. (q0 p0)		Індекс фізичного обсягу продукції, iq
	Молоко Сир		60 000 125 000		1,1 1,2
Разом		185 000		—

Індекс фізичного обсягу товарообігу становитиме:

Тобто фізичний обсяг реалізації продукції збільшився на 16,8 %.

Аналогічно можна перетворити агрегатний індекс цін:

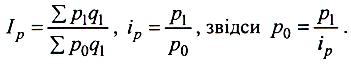(7.7)

Підставивши в знаменник це значення замість р₀, одержимо середній гармонійний індекс цін, тотожний агрегатному:

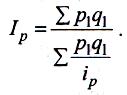(7.8)

Загальне правило перетворення агрегатних індексів у середні гармонійні таке: для того щоб середні гармонійний індекс був тотожний агрегатному, вагами індивідуальних індексів повинні бути доданки чисельника вихідного агрегатного індексу.

У розрахунках середніх індексів перетворюють так звані сконструйовані величини (p₀q₁), а не реальні (звітні) (p₀q₀, p₁q₁).

Розглянемо розрахунок на пpиклaдi (табл. 7.3).

Таблиця 7.3

Обсяг товарообігу магазину і зміна цін

Спорттовари	Обсяг товарообігу званого періоду, тис. грн., p1q1	Розмір зміни цін, %	Індивідуальні індекси цін, ip
Спортивний одяг	450	-2	0,98 (1 - 0,02)
інвентар	920	+5	1,05 (1 + 0,05)
Разом	1370	—	—

Обчислимо загальний індекс цін:

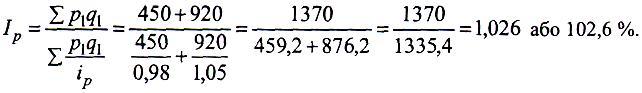
Товарообіг за рахунок зростання цін на спорттовари у звітному році збільшився на 2,6 %.

До розрахунку середніх індексів звертаються, коли відсутні необхідні дані для обчислення агрегатного індексу.

У податковій діяльності часто виникає необхідність проведення аналізу динаміки за сукупністю порушень податкового законодавства, у ході якого використовують формули, побудовані за методикою агрегатного індексу. Наприклад, відповідно до даних статистичної звітності «Звіт про порушення податкового законодавства і результати роботи» протягом січня було зафіксовано 25 випадків несплати податку на прибуток, 20 випадків несплати податку за землю, 56 ухилень від сплати податків, 32 випадки несплати ПДВ, а в лютому скоєні відповідні порушення податкового законодавства в кількості 18, 22, 61 та 43. Якщо кількість порушень податкового законодавства за їх видами помножити на їх бали (а це можуть бути й індивідуальні індекси), то одержимо умовну кількість порушень податкового законодавства. Тоді можна побудувати, наприклад, агрегатний індекс .порушення податкового законодавства (І_п.п.з.), який матиме такий вигляд:

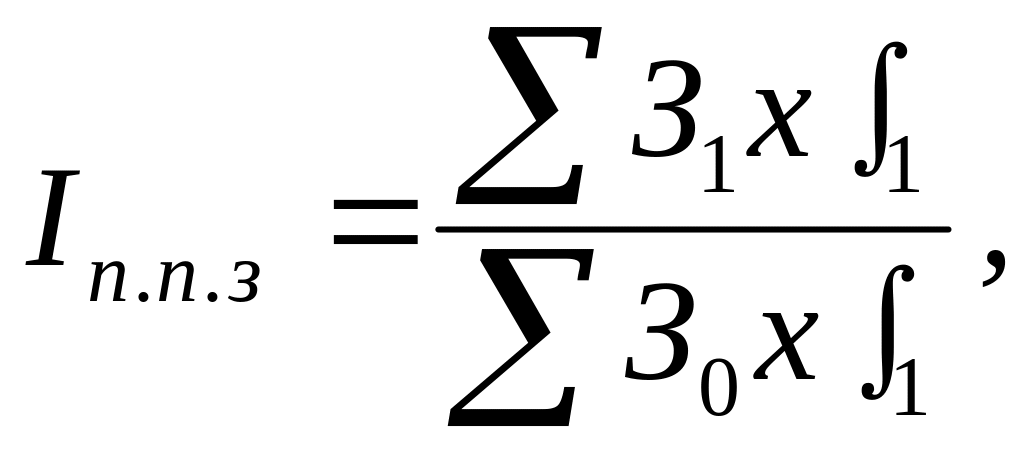(7.9)

де З₀, З₁ — кількість порушень податкового законодавства кожного виду відповідно в базисному та звітному періодах;

ƒ₁ — бали грубості порушення податкового законодавства (бажано, щоб вони були одні і ті самі для обох періодів).

Тобто в нашому прикладі:

(7.10)

Індекс показує, що порушення податкового законодавства у лютому порівняно з січнем знизилася на 6 % завдяки зменшенню порушень податкового законодавства за видами.

Такий аналіз проводять як у динаміці, так і по регіонах, що дає можливість мати не тільки кількісну, а й якісну характеристику податкової діяльності. Використовуючи такі індекси, наприклад в разі рівної кількості порушень податкового законодавства, можна відстежити причину формування рівня порушень податкового законодавства в кожному регіоні, місті чи районі.

Аналогічно будуються й інші індекси податкової статистики. Наприклад, індекс покарань за порушення податкового законодавства (І_п.п.п.з.) має такий вигляд:

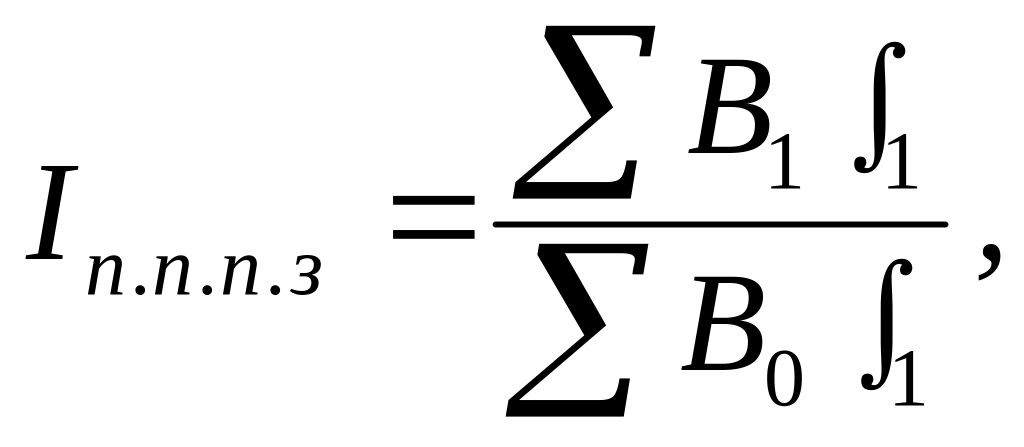(7.11)

де В₀, В₁ — кількість осіб, що були оштрафовані за несплату податків відповідно в базисному і звітному періодах;

ƒ₁ — бали порушення податкового законодавства.

За допомогою зіставлення індексів покарань за порушення податкового законодавства на основі рівня штрафів і реально призначених податковим органом строків сплати штрафів можна оцінити ступінь розбіжності податкової практики і положень чинного законодавства.

4. Для факторного аналізу динаміки середніх величин у податковій статистиці використовують індекси змінного, постійного складу і структурних зрушень.

Індекс середніх розмірів називається індексом змінного складу. Він показує зміну середньої величини, зумовлену дією двох факторів — змінами окремих рівнів показника і структури сукупності.

Індекс змінного складу можна розкласти на два аналітичних індекси-співмножники, кожний із яких відображає вплив тільки одного фактора. Один індекс-співмножник показує, як змінився б середній рівень показника за рахунок зміни індивідуальних рівнів якісного показника при постійній структурі сукупності, і називається індексом постійного складу. Інший індекс-співмножник показує, як змінився б середній рівень показника за рахунок зміни структури сукупності при збереженні базисних рівнів якісного показника. Це індекс структурних зрушень.

Індекс змінною складу дорівнює добутку індексу постійного (фіксованого) складу на індекс структурних зрушень:

(7.12)

Розглянемо розрахунок цієї системи індексів на прикладі (табл. 7.4).

Таблиця 7.4

Чисельність працівників податкових органів та рівень середньої зарплати

Група працівників податкових органів	Базисний період		Звітний період
	Середня місячна чисельність працівників податкових органів, чол. (Ч0)	Середня заробітна плата, грн. (3о)	Середня місячна чисельність працівників податкових органів, чол. (Ч1)	Середня заробітна, плата, грн. (31)
1 2	15 20	200 250	16 25	230 300
Разом	35	-	41	-

Обчислимо середню заробітну плату по двох і групах працівників у базисному і звітному періодах:

Індекс середньої заробітної плати (змінного складу) становить:

Середня зарплата працівників податкових органів у звітному періоді збільшилася на 19,3 % за рахунок одночасного впливу двох факторів — зміни середньої місячної заробітної плати по кожній групі працівників і зміни складу груп працівників (група працівників із меншою зарплатою знизилася з 43 до 39 % у звітному періоді порівняно з базисним). Індекс зарплати постійного складу дорівнює:

У середньому зарплата працівників податкових органів у звітному періоді підвищилася на 18,3 % порівняно з базисним тільки за рахунок динаміки середньомісячної зарплати кожної групи працівників (склад працівників постійний).

Обчислимо індекс впливу зміни структури сукупності на рівень зарплати:

де - середня зарплата працівників податкових органів у звітному періоді розрахована за середньомісячною зарплатою окремих груп працівників у базисному періоді.

Зміна структури (складу) працівників привела до зростання середньої зарплати у звітному періоді порівняно з базисним на 0,8 %.

Необхідно зазначити особливості застосування індексів у фінансово-податковій статистиці. Варто мати на увазі, що застосування загальних індексів у фінансово-податковій статистиці для характеристики середньої динаміки порушень податкового законодавства, які складаються із різних у якісному плані категорій, абсолютно неприпустиме. Обчислення середнього індексу за допомогою певних співмножників (скажімо, ваги податкових покарань) із числа таких різнорідних за економічною небезпекою порушень податкового законодавства, як ухилення від сплати податків тощо, було б типовим прикладом математичного формалізму повного ігнорування якісного аналізу.

Тому якщо обчислення загальних індексів допустиме в різних сферах економіки, промисловості, торгівлі та ін., так як тут якісно обґрунтовано застосування відповідних співмножників (ваг), то у податковій статистиці ніякі співмножники (ваги) не можуть усунути розходження між ухиленням від сплати різних видів податків.

Проте фінансистам часто доводиться мати справу з індексами у практиці податкових адміністрацій i податкових інспекцій, наприклад при розслідуванні справ про різні види ухилення від оплати податків.

Аналогічно розраховуються й індекси, що безпосередньо характеризують податкову діяльність. Наприклад, динаміку середнього рівня порушень податкового законодавства по регіонах можна аналізувати за допомогою такої індексної системи:

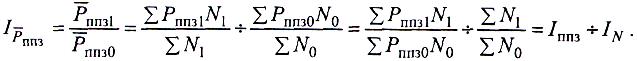(7.13)

Даний індекс показує, як змінився середній рівень порушень податкового законодавства за сукупністю регіонів у звітному періоді порівняно з базисним:

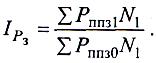(7.14)

Цей індекс показує, як змінився середній рівень порушень податкового законодавства за сукупністю регіонів у звітному періоді порівняно з базисним завдяки зміні рівня порушень у кожному регіоні.

(7.15)

Даний індекс показує, як змінився середній рівень порушень податкового законодавства за сукупністю регіонів у звітному періоді порівняно з базисним завдяки змінам, що відбулися у структурі чисельності населення peгioнiв.

Взаємозв’язок індексів:

(7.16)

де - індекс середнього рівня порушень податкового законодавства;

- індекс рівня злочинності;

I_N - індекс структурних зрушень;

Р_ппз0, Р_ппз1 - рівень порушень податкового законодавства та чинники відповідно в базисному й звітному періодах;

3 - кількість зареєстрованих порушень податкового законодавства;

N - чисельність населення.

За допомогою зазначеної індексної системи визначають динаміку середнього piвня порушень податкового законодавства та чинники, що й породжують.

Знання індексів необхідне для орієнтування в ряді важливих економіко-податкових питань.