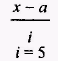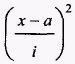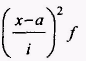Для не згрупованих даних
II випадок
-
Кількість платників податків, х
х – х
х = 47
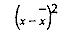
10
-37
1369
20
-27
729
25
-22
484
35
-19
361
40
-7
49
45
— 2
4
55
8
64
60
13
169
80
33
1089
100
53
2809
Разом
—
7127
Отже,
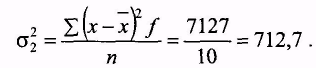
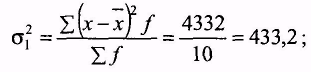
Тоді
платник податків;
платників
податків.
Середнє квадратичне відхилення у першому випадку менше, ніж у другому.
Дисперсія і середнє квадратичне відхилення є найпоширенішими й загальновідомими абсолютними показниками варіації досліджуваної ознаки.
Ці показники мають математичні властивості, які допомагають спростити розрахунок:
• дисперсія ознаки дорівнює різниці між середнім квадратом значення ознаки (х2 )1 квадратом їх середньої ( х2 ):
(5.22)
Цей спосіб розрахунку ефективний у тому разі, якщо варіанти виражені невеликими числами і їх небагато;
дисперсія не змінюється, якщо усі варіанти збільшити або зменшити на якесь постійне число а;
якщо усі варіанти поділити (помножити) на будь-яке число (і), то дисперсія зменшиться (збільшиться) у і2 разів, а середнє квадратичне відхилення - відповідно в і разів.
На цих властивостях дисперсії заснований спрощений спосіб обчислення середнього квадратичного відхилення. Розглянемо розрахунок на прикладі (табл. 5.8):
Таблиця 5.8
Розподіл порушень податкового законодавства за віком платників податків
Вік платників податків |
Кількість порушень податкового законодавства, % до результату, f |
Середина інтервалу, х |
х — а о = 28 |
|
|
|
|
До 18 |
3 |
13 |
-15 |
-3 |
-9 |
9 |
27 |
19-23 |
11 |
18 |
-10 |
-2 |
-22 |
4 |
44 |
24-28 |
22 |
23 |
-5 |
-1 |
22 |
1 |
22 |
29-33 |
26 |
28 |
0 |
0 |
0 |
0 |
0 |
34-38 |
19 |
33 |
5 |
1 |
19 |
1 |
19 |
39-43 |
10 |
38 |
10 |
2 |
20 |
4 |
40 |
44-48 |
5 |
43 |
15 |
3 |
15 |
9 |
45 |
49-53 |
4 |
48 |
20 |
4 |
16 |
16 |
64 |
Разом |
100 |
|
|
|
17 |
|
261 |
Порядок розрахунку такий:
інтервальний ряд перетворюємо у дискретний;
знаходимо відхилення х - а, де а дорівнює варіанті, що має найбільшу частоту, або варіанті, розташованій в середині ряду;
відхилення х - а зменшуємо в і разів, де і - найбільший загальний дільник. У рівноінтервальному ряду і дорівнює інтервалу;
з
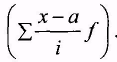меншені
варіанти множимо на частоти і визначаємо
суму добутку
Знаходимо момент першого порядку:
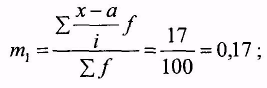
зменшені варіанти підносимо до квадрата;
піднесені до квадрата зменшені варіанти множимо на відповідні частоти, знаходимо суму добутків і обчислюємо момент другого порядку:
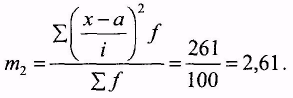(5.24)
Середнє квадратичне відхилення визначається за формулою:
де m2 - середній квадрат значення ознаки (х2);
m12 - квадрат середнього значення ознаки (х2).
Поставивши значення, одержуємо:
років.
Вік порушників податкового законодавства відхиляється (варіює) від середнього віку (29 років) на ±8 років:
років.
Усі розглянуті показники варіації характеризують абсолютний розмір відхилення і виражаються в тих самих одиницях виміру, в яких виражені варіанти і середня. Для порівняльної характеристики варіації рядів із різними рівнями застосовується відносний показник варіації — коефіцієнт варіації.
Коефіцієнт варіації — це відношення середнього квадратичного відхилення до середньої величини, виражене у відсотках:
(5.25)
Він більш наочно характеризує варіацію ознаки і є певною мірою критерієм надійності середньої. Якщо коефіцієнт варіації більший 40 % (а в деяких випадках 33 %), то це означає, що середня не дуже надійна для даної сукупності і сукупність за цією ознакою неоднорідна.
Обчислимо коефіцієнт варіації для наших прикладів:
Надійність середньої і у першому, і в другому випадках невелика, але в першої трохи вища. Щодо сукупності розподілу порушників податкового законодавства за віком суб'єктів, то вона однорідна і середня надійна, типова, тому що коефіцієнт варіації менший 33 %:
