I випадок
-
Кількість платників податків, х
Кількість податкових інспекторів, f
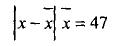
20
2
27
54
30
1
17
17
40
3
7
21
53
1
6
6
70
1
23
23
75
1
28
28
80
1
33
33
Разом
10
182
Отже,
середнє лінійне відхилення дорівнює:
платників податків.
Таблиця5.5
Розподіл платників податків за податковими інспекторами, що їх обслуговують
II випадок
-
Кількість платників податків, x
Кількість податкових інспекторів, f
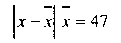
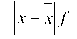
10
1
37
37
20
1
27
27
25
1
22
22
35
1
12
12
40
1
7
7
45
1
2
2
55
1
8
8
60
1
13
13
80
1
33
33
100
1
53
53
Разом
10
-
214
Отже,
середнє відхилення дорівнює:
платник
податків.
Середнє лінійне відхилення менше в першому випадку, що підтверджує той факт, що сукупність більш однорідна і в середньому більш надійна, ніж у другій сукупності. Через ігнорування знака цей показник варіації менш популярний, ніж дисперсія і середнє квадратичне відхилення.
Дисперсія — це середня величина із квадратів відхилень варіант від середньої величини (2), а корінь квадратний із дисперсії називається середнім квадратичним відхиленням.
Дисперсія обчислюється за формулами: для не згрупованих даних:
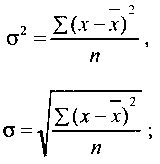(5.19)
для згрупованих даних, коли частоти різні:
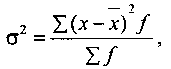
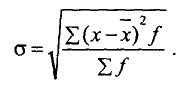(5.20)
Визначимо ці показники для нашого прикладу (табл. 5.6, 5.7). Розрахунок дисперсії і середнього квадратичного відхилення.
Таблиця 5.6
Для згрупованих даних
I випадок
Кількість платників податків, х |
Кількість податкових інспекторів, f |
х - х х = 47 |
|
|
20 |
2 |
-27 |
729 |
1458 |
30 |
1 |
-17 |
289 |
289 |
40 |
3 |
-7 |
49 |
147 |
53 |
1 |
6 |
36 |
36 |
70 |
1 |
23 |
529 |
529 |
75 |
1 |
28 |
784 |
784 |
80 |
1 |
33 |
1089 |
1089 |
Разом |
10 |
— |
— |
4332 |
Таблиця 5.7