38. Методы численного интегрирования: постановка задачи, метод трапеций.

Ещё одним простейшим полиномом является линейная функция. Если она выбрана совпадающей с в концах отрезка a и b, то получаем трапецию.

Площадь этой трапеции (интеграл от линейной функции), используемая в качестве приближения к значению интеграла от , определяется по формуле:

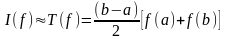. (5.3)

Эта формула (5.3) известна как формула трапеции.

Р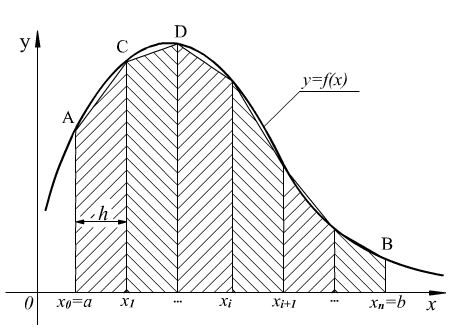 ис. 5.3. Метод трапеции.

Для того чтобы найти приближенное значение площади S, разделим отрезок интегрирования [a,b] на n равных частей длины (рис.5.3.). В точках разбиения 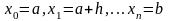проводим ординаты 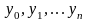до пересечения с кривой , т.е. , 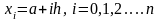. Концы ординат соединяем прямолинейными отрезкам, т.е. на каждом отрезке разбиения дугу графика подинтегральной функции заменяем стягивающей ее хордой (линейная интерполяция), и получим трапецию.

Тогда площадь криволинейной трапеции 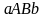приближенно можно считать равной площади фигуры, ограниченной ломаной линией 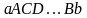. Площадь этой фигуры, которую мы обозначим как S, равна сумме площадей трапеций:

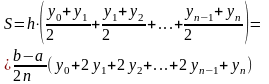
Таким образом, для интервала и шага интегрирования h полная формула приближенного значения интеграла будет записана в виде:

(5.4)

где n - число разбиений для интервала и точка совпадает с , а точка x_n совпадает с b.

39. Методы численного интегрирования: постановка задачи, метод Симпсона.

Более высокая точность определения численного значения определенного интеграла получается при аппроксимации функции f(x) квадратичным интерполяционным полиномом, который совпадает с f(x) в крайних точках a и b, а также в средней точке . Интеграл от этого квадратичного полинома выражается формулой:

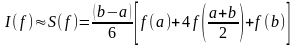, (5.5)

к оторая называется формулой Симпсона.

Рис. 5.4. Метод Симпсона.

В методе Симпсона площадь криволинейной трапеции рассчитывается как сумма площадей ряда криволинейных трапеций, у которых криволинейная сторона представляет собой участок параболы. Это можно видеть на рис.5.4.

Каждая парабола может быть проведена только через три граничные точки, принадлежащие двум соседним отрезкам. Поэтому число участков разбиения отрезка [a,b] в отличие от предыдущих методов обязательно должно быть четным. Таким образом, вместо каждых двух элементарных прямолинейных трапеций будем рассматривать одну элементарную трапецию, ограниченную параболической дугой. Исходя из этого, определенный интеграл на случай разбиения интервала на n участков с шагом h. приближенно вычисляется по формуле:

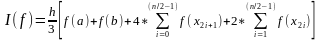(5.6)

– полная формула Симпсона.

Таким образом, для реализации метода прямоугольников, трапеции и Симпсона для вычисления определенного интеграла необходимо:

Задать в явном виде определенный интеграл, площадь которого необходимо определить. После этого задаются пределы интегрирования, и шаг интегрирования. Затем проводится расчет по формулам (5.2), (5.4) и (5.6).

Для метода Симпсона число разбиений n должно быть четным, что подлежит проверке при составлении программы.

40. Методы численного интегрирования: постановка задачи, методы Монте–Карло.

Метод Монте-Карло – метод решения, вычислительная сложность которого не сильно зависит от размерности функции.

Первый вариант

Его можно интерпретировать как статистический вариант метода прямоугольников (рисунок 3). Только в качестве узла x₀ берется случайное число, равномерно распределенное на интервале интегрирования . Вследствие случайного узла x₀ погрешность интеграла также будет носить случайный характер.

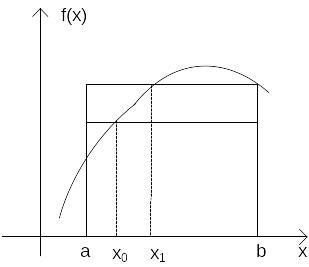
Рисунок 3

Проведя N вычислений со случайными узлами x_i результат усредняется и усредненное значение принимается за приближенное значение интеграла (4.6.1):

(4.6.1)

Погрешность интеграла будет уменьшаться с ростом числа испытаний N по закону .

Второй вариант

Вычисляемый интеграл приводится к виду (4.6.2)

(4.6.2)

где на интервале . Тогда две случайные величины x_i и x_j можно рассматривать как координаты точек в единичном квадрате. При равномерном распределении точек в квадрате за приближенное значение интеграла принимается отношение количества точек S, попавших под кривую y=f(x) к общему числу испытаний N (4.6.3) (рисунок 4):

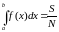(4.6.3)

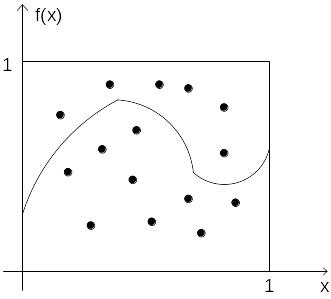
Рисунок 4