
- •12. Основные операции над данными в языке си (операция присваивания, арифметические операции).
- •15. Функции пользователя: понятие, операторы определения, описания и вызова функции. Формальные и фактические параметры.
- •24. Численные методы решение алгебраических уравнений: метод Ньютона, модифицированный метод Ньютона.
- •26. Численные методы решение алгебраических уравнений: постановка задачи, метод простых итераций.
- •27. Численные методы решения систем линейных уравнений (слау): проверка корректности постановки задачи.
- •28. Численные методы решения систем линейных уравнений (слау): постановка задачи, метод Гаусса.
- •30. Численные методы решения систем линейных уравнений (слау): постановка задачи, метод Зейделя.
- •31. Численные методы восстановления функций: постановка задачи. Понятие аппроксимации, интерполяции и экстраполяции.
- •32. Численные методы восстановления функций: интерполяция полиномом Лагранжа. Интерполяционные формулы Лагранжа и Ньютона без вывода.
- •33. Численные методы восстановления функций: погрешность интерполирования (остаточный член интерполяционной формулы и оптимальный выбор узлов).
- •35. Численные методы восстановления функций: метод наименьших квадратов.
- •37. Методы численного интегрирования: постановка задачи, метод прямоугольников
- •38. Методы численного интегрирования: постановка задачи, метод трапеций.
- •39. Методы численного интегрирования: постановка задачи, метод Симпсона.
- •40. Методы численного интегрирования: постановка задачи, методы Монте–Карло.
- •41. Решение математических задач в excel: алгебраических уравнений, слау.
- •42. Решение математических задач в пакете MathCad: алгебраических уравнений, слау, восстановления функции, вычисления определенных интегралов
- •43. Понятие информационной системы. Виды информационных систем
- •44. Понятие базы данных. Виды баз данных. Модели данных
- •45. Элементы баз данных. Принципы создания базы данных. Языковые средства баз данных.
- •46. Основы работы в субд foxpro: типы файлов, системный интерфейс.
- •47. Структура команды foxpro. Основные команды foxpro: открытие базы данных (бд), добавление записей, редактирование бд, просмотр содержимого бд.
- •53. Команды присваивания и управления.
- •54. Команды организации циклов Цикл с условием с несколькими:
- •Цикл с параметром:
- •Цикл сканирования базы данных:
- •55. Функции и процедуры классы переменных.
- •58. Протоколы передачи данных в сети.
- •59. Каналы связи в сети. Типы кабелей. Беспроводная среда.
- •60. Классификация компьютерных сетей.
- •61. Локальные сети: понятие и особенности.
- •62. Особенности организации локальной сети: одноранговая сеть, сеть с выделенным сервером.
- •63. Топология локальных сетей: понятие и виды.
- •64. Глобальные сети: понятие и особенности.
- •65. Структура и основные принципы работы в сети Интернет.
- •66. Адресация в Интернет.
26. Численные методы решение алгебраических уравнений: постановка задачи, метод простых итераций.
Предположим, что уравнение (1) при помощи некоторых тождественных преобразований приведено к виду (2):
 (1)
(1)
 (2)
(2)
Пусть
известно начальное приближение к корню
 ,
тогда подставим его в правую часть
уравнения (2) и получим новое приближение:
,
тогда подставим его в правую часть
уравнения (2) и получим новое приближение:
 (3)
(3)
Затем
аналогичным образом получим
 и т.д.:
и т.д.:
 (4)
(4)
Заметим:
тот факт, что
 корень уравнения
,
означает, что
есть
абсцисса точки пересечения графика
корень уравнения
,
означает, что
есть
абсцисса точки пересечения графика
 с
прямой
с
прямой
 .
.
Необходимо установить, при каких условиях итерационный процесс будет сходиться к корню уравнения .
Рассмотрим процесс графически (рисунок 1).

Рисунок 1
Из
графиков видно, что при
 и
при
и
при
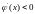 возможны
как сходящиеся, так и расходящиеся
итерационные процессы.
возможны
как сходящиеся, так и расходящиеся
итерационные процессы.
Скорость
сходимости зависит от абсолютной
величины производной функции
 .
Чем меньше
.
Чем меньше
 вблизи корня, тем быстрее сходится
процесс.
вблизи корня, тем быстрее сходится
процесс.
Установим теперь критерий сходимости математически.
Будем считать, что в итерационной формуле (4)
 (5)
(5)
где
 ,
,
 - отклонения k
и k+1приближения
к корню. Если процесс уточнения
осуществляется вблизи корня
,
то функцию
можно
приближенно представить двумя членами
ряда Тейлора. Тогда итерационная формула
(4) примет вид (6):
- отклонения k
и k+1приближения
к корню. Если процесс уточнения
осуществляется вблизи корня
,
то функцию
можно
приближенно представить двумя членами
ряда Тейлора. Тогда итерационная формула
(4) примет вид (6):
 (6)
(6)
но
так как
является
корнем уравнения, то
 и,
следовательно (7),
и,
следовательно (7),
 (7)
(7)
Для того чтобы итерационный процесс был сходящимся, необходимо выполнить условие (8)
 (8)
или
(8)
или
 Переход
от уравнения (1) к уравнению (2) можно
осуществить разными способами в
зависимости от вида функции
Переход
от уравнения (1) к уравнению (2) можно
осуществить разными способами в
зависимости от вида функции
 .
При таком переходе необходимо построить
функцию
так,
чтобы выполнялось условие сходимости
(8).Рассмотрим один из общих алгоритмов
перехода от уравнения (1) к уравнению
(2).Умножим левую и правую части уравнения
(1) на произвольную константу
.
При таком переходе необходимо построить
функцию
так,
чтобы выполнялось условие сходимости
(8).Рассмотрим один из общих алгоритмов
перехода от уравнения (1) к уравнению
(2).Умножим левую и правую части уравнения
(1) на произвольную константу
 и
добавим к обеим частям неизвестное
и
добавим к обеим частям неизвестное
 .
При этом корни исходного уравнения не
изменятся (9):
.
При этом корни исходного уравнения не
изменятся (9):
 (9)
(9)
Введем
обозначение
 (10)
(10)
и перейдем от соотношения (9) к уравнению (2).
Произвольный
выбор константы
позволит
обеспечить выполнение условия сходимости
(8). Желательно выбрать величину
такой,
чтобы
 ,
тогда сходимость итерационного процесса
будет двухсторонней. В этом случае в
наиболее простом виде можно представить
критерий окончания итерационного
процесса.
,
тогда сходимость итерационного процесса
будет двухсторонней. В этом случае в
наиболее простом виде можно представить
критерий окончания итерационного
процесса. (11)
(11)
где
 -
заданная абсолютная погрешность
вычисления корня. Если функция
выбрана
в виде (1.33), то производная по
от
этой функции будет
-
заданная абсолютная погрешность
вычисления корня. Если функция
выбрана
в виде (1.33), то производная по
от
этой функции будет
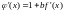 (12).Наибольшую скорость сходимости
получим при
(12).Наибольшую скорость сходимости
получим при
 ,
тогда
,
тогда
 и
итерационная формула (4) переходит в
формулу Ньютона (13)
и
итерационная формула (4) переходит в
формулу Ньютона (13)
27. Численные методы решения систем линейных уравнений (слау): проверка корректности постановки задачи.
Исследование
устойчивость задачи
сводится к исследованию зависимости
ее решения от правых частей
 и элементов
и элементов
 матрицы А. Для того чтобы можно было
говорить о непрерывной зависимости
вектора решений от некоторых параметров,
необходимо на множестве
матрицы А. Для того чтобы можно было
говорить о непрерывной зависимости
вектора решений от некоторых параметров,
необходимо на множестве
 -
мерных векторов принадлежащих линейному
пространству H,
ввести метрику.
-
мерных векторов принадлежащих линейному
пространству H,
ввести метрику.
В
линейной алгебре предлагается определение
множества метрик

норма
норма
 из которого легко получить наиболее
часто используемые метрики
из которого легко получить наиболее
часто используемые метрики
при
р=1,
 ,
,
при
 ,
,
 ,
,
при
 ,
,
 .
.
Подчиненные
нормы матриц определяемые как
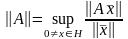 , соответственно запишутся в следующем
виде:
, соответственно запишутся в следующем
виде:
 ,
,
 ,
,
 .
.
Обычно рассматривают два вида устойчивости решения системы (1):первый по правым частям, второй по коэффициентам системы(1) и по правым частям..
Наряду с исходной системой (1) рассмотрим систему с «возмущенными» правыми частями
 ,
,
где

возмущенная правая часть системы, а
возмущенная правая часть системы, а
 возмущенное решение.
возмущенное решение.
Можно получить оценку, выражающую зависимость относительной погрешности решения от относительной погрешности правых частей
 ,
,
где

число обусловленности матрицы А ( в
современной литературе это число
обозначают как
число обусловленности матрицы А ( в
современной литературе это число
обозначают как
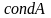 )
Если число обусловленности велико (
)
Если число обусловленности велико (
 ),
то говорят, что матрица А плохо обусловлена.
В этом случае малые возмущения правых
частей системы (1), вызванные либо
неточностью задания исходных данных,
либо вызванные погрешностями вычисления
существенно влияют на решение системы.
Грубо говоря если погрешность правых
частей
),
то говорят, что матрица А плохо обусловлена.
В этом случае малые возмущения правых
частей системы (1), вызванные либо
неточностью задания исходных данных,
либо вызванные погрешностями вычисления
существенно влияют на решение системы.
Грубо говоря если погрешность правых
частей
 ,
то погрешность решения будет
,
то погрешность решения будет
 .
Более подробно о свойствах числа
обусловленности и оценка его величины
можно прочитать в [3].
.
Более подробно о свойствах числа
обусловленности и оценка его величины
можно прочитать в [3].
Если возмущение внесено в матрицу А, то для относительных возмущений решения запишем
 .
.
