39. Вариация и её свойства.

Определение 2:

Приращением или вариацией аргумента функционала называется разность между двумя функциями , где меняется произвольно в некотором классе функций.

Определение 3:

Функционал непрерывен при в смысле близости ого порядка, если такое, что имеет место неравенство

при

,

,

…

.

Функция берётся из класса функций, на котором функционал определён.

Определение 4:

Функционал называется линейным , если выполняются следующие условия:

1. , где постоянная.

2

Например, .

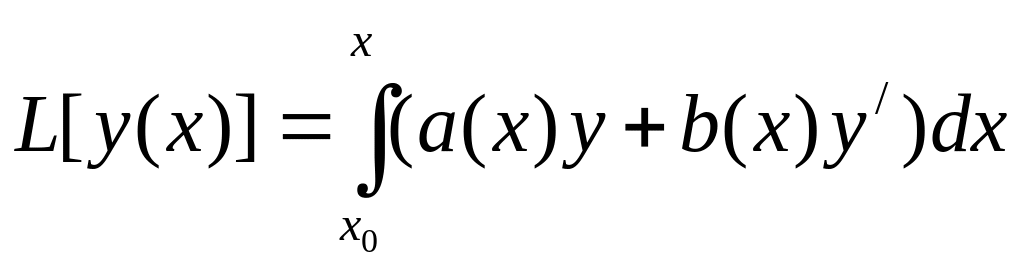Определение 5:

Если приращение функционала представимо в таком виде, где линейный по отношению к функционал и при , то линейная по отношению к часть приращения функционала, т.е. называется вариацией функционала и обозначается .

Итак, вариация функционала – это главная, линейная по отношению к часть приращения функционала.

При исследовании функционалов, вариация играет ту же роль, что и производная при исследовании функций.

Вообще говоря, упрощения исследования функционалов дают почти эквивалентное определение вариации функционала.

по при , т.е. .

Действительно, производная от по при равна:

.

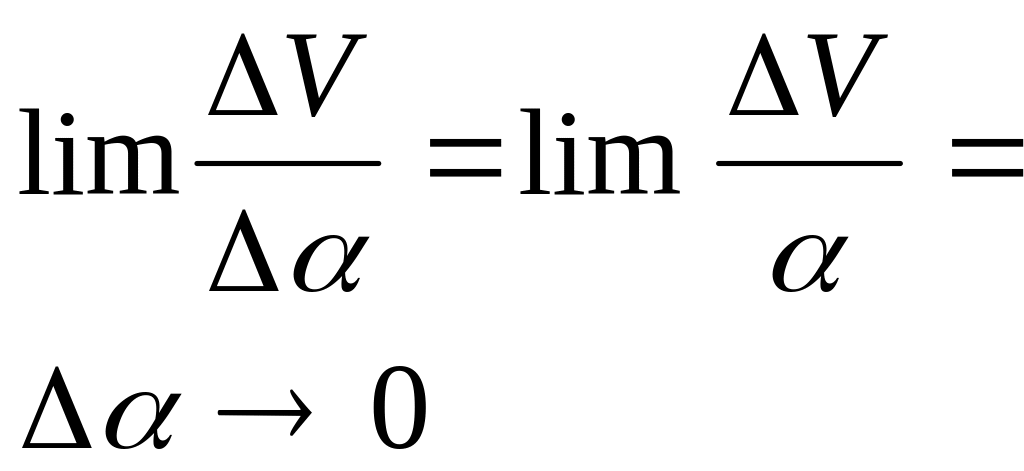
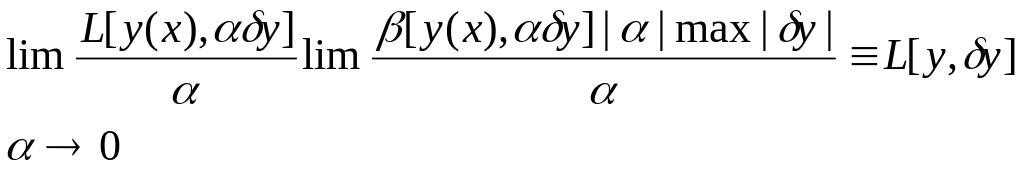Так как , а

Если существует вариация в смысле главной части приращения функционала, то существует и вариация в смысле производной по параметру при . Второе определение несколько шире первого, так как не всегда можно выделить главную линейную часть приращения функционала.

Определение 6:

Функционал достигает на кривой максимума(минимума), если значения функционала на любой близкой от кривой, больше(не меньше), чем , т.е. .

Если ( ) и только при , то говорят, что на кривой достигается строгий максимум (минимум).

Теорема:

Если функционал , имеющий вариацию, достигает максимума или минимума при , где внутренняя точка область определения функционала, то при , .

При одинаковых и функционал является функцией от , которая при по предположению имеет максимум или минимум. Тогда или

,

В определении максимума или минимума надо указывать, какого порядка близость имеется в виду. Если функционал достигает максимума или минимума по отношению ко всем кривым, для которых мал, то максимум или минимум называется сильным.

Если же лишь по отношению к кривым, близким к в смысле близости первого порядка, т.е. ещё мал и , то максимум или минимум называется слабым.

Замечание:

Если на кривой достигается экстремум, то не только ,

но и , где любое семейство допустимых кривых, причём при и функция должна приращаться в и . Эта производная, конечно, не совпадает с вариацией функционала, но обращается в нуль одновременно с , на кривых, реализующих экстремум функционала, это будет использовано в дальнейшем при исследовании функционалов на экстремум.

ЛЕКЦИЯ 15:

40. Основная лемма вариационного исчисления.

Если для каждой непрерывной функции ,

, где непрерывна на отрезке отрезке , то на том же отрезке.

Доказательство:

Предположим, что , .

Тогда из непрерывности следует, что существует окретность точки , где сохраняет знак . Выбрав функцию , сохраняющую такой же знак в этой окрестности, и равноё нулю вне этой окрестности, получим:

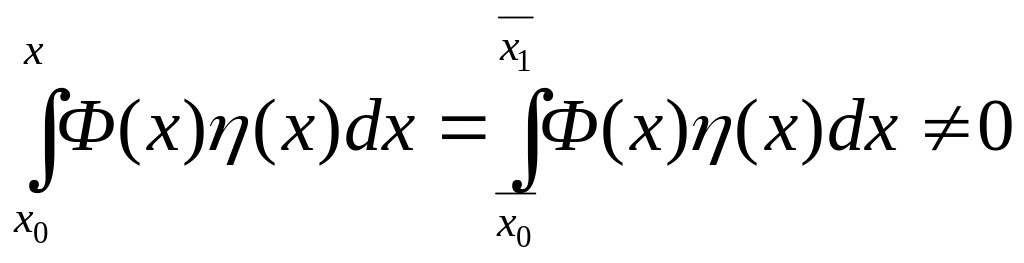
Пришли к противоречию. Следовательно, .

Замечание:

Аналогично доказывается, если непрерывна в области на плоскости и при любом непрерывной в .