Глава 3: Линейные системы дифференциальных уравнений с постоянными коэффициентами.

, (1), где - постоянные вещественные числа, - непрерывны в интервале (a,b).

Так как общее решение неоднородной системы связано с построением общего решения соответствующей однородной системы, то, естественно, сначала рассмотрим однородную систему , (2).

Фундаментальная система решений, из ранее доказанного, существует в интервале .

Для системы (2) всегда можно построить ФСР из элементарных целых функций.

Решение системы (2) будем искать в виде , (3).

Подставляя (3) в (2), получаем , .

Сокращая на , имеем линейную однородную систему относительно , .

(4).

Нетривиальное решение система (4) имеет, когда определитель её равен нулю, т.е. (5).

Уравнение (5) называется характеристическим уравнением системы (2), а корни его называются характеристическими числами. представляет собой многочлен степени n относительно λ.

Случай 1. Все корни характеристического многочлена - действительные и различные, т.е. .

Покажем, что в этом случае ранг матрицы

равен n-1.

Рассмотрим:

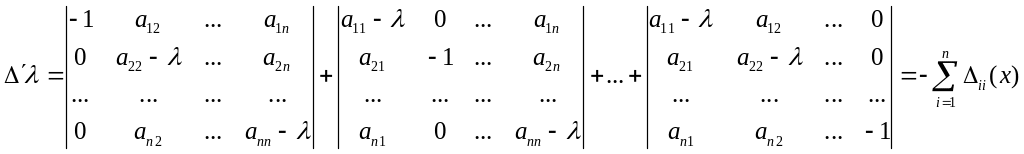
где - алгебраические дополнения элемента определителя .

Следовательно, хоть один из определителей (n-1)-го порядка отличен от нуля.

Система (4) имеет ненулевое решение, которое определяется с точностью до множителя. Таким образом, получим n решений системы (2).

(6) - ФСР системы (2).

Поэтому, в силу основной теоремы, общее решение системы (2) в области , имеет вид:

(7).

Пример.

(8).

Подставляя в систему (4), получаем:

.

Аналогично находим при :

.

.

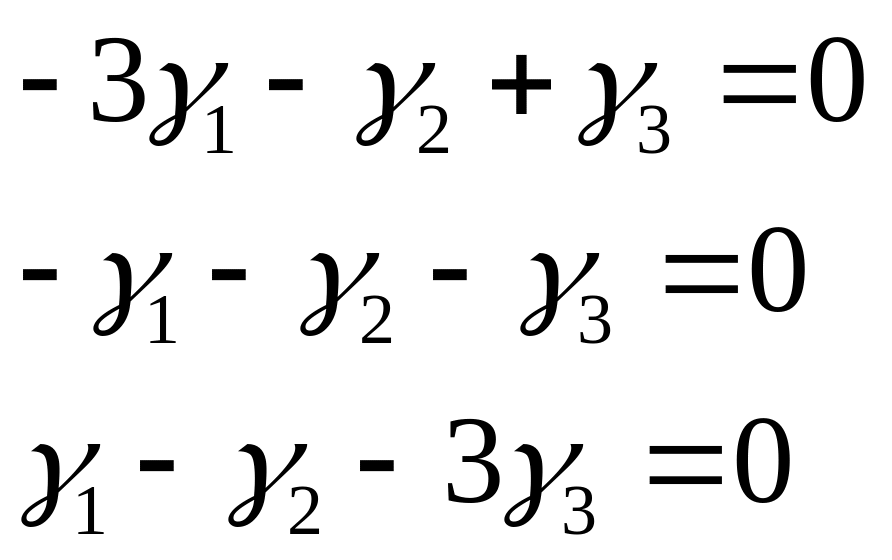
(9) – общее решение системы (8).

Случай 2. Все корни различны, но среди них имеются комплексные.

a + ib u a – ib - простые корни характеристического уравнения. Корню a + ib, согласно формуле (3), соответствует решение

- комплексные числа. Поэтому y₁,..., y_n – комплексное решение.

Отделяя в нём вещественную и мнимую части, получим два вещественных решения. Сопряжённый корень a – ib не порождает новых вещественных решений.

Итак, паре комплексно сопряжённых корней соответствует два вещественных линейно независимых решения.

Пример. (10)

(11) – общее решение данной системы.

Случай 3. Среди корней характеристического уравнения имеются кратные корни.

Как построить в этом случае ФСР для системы (2) даёт ответ следующая теорема.

Теорема.

Если есть характеристическое число кратности k, то ему соответствует решение вида , где P₁(x), P₂(x),..., P_n(x) – полиномы от х степени, не превышающей k-1, имеющие в совокупности k произвольных коэффициентов. Полиномы могут вырождаться в постоянные числа. В таком случае k-кратному характеристическому числу будет соответствовать решение вида . Но среди коэффициентов k коэффициентов являются произвольными.

Пример.

(12)

λ=-2 - корень кратности два, ему соответствуют решения

(13). Сокращая их на и подставляя в систему (12), получаем:

(14).

Сравнивая в системе (14) коэффициенты при одинаковых степенях, получаем следующие соотношения:

.

Положим : .

Положим : .

Таким образом, (15).

(15) – общее решение системы (12).

ЛЕКЦИЯ 10: