
- •Метрология и технические измерения.
- •Задачи метрологии.
- •Основные и производные единицы в си
- •Метрологические характеристики средств измерения.
- •По способу получения результата измерения различают на:
- •Погрешность измерения.
- •Основная и дополнительная погрешности.
- •Классификация погрешностей по свойствам
- •Центральный момент первого порядка.
- •Центральный момент второго порядка.
- •Погрешность косвенных измерений
- •Выбор средства измерения по точности
Центральный момент первого порядка.
![]()
Сколько бы не измеряли все моменты располагаются около МХ при n.
Центральный момент второго порядка.
![]() ДХ – дисперсия
ДХ – дисперсия
![]() -
характеризует величину рассеивания
результатов наблюдения.
-
характеризует величину рассеивания
результатов наблюдения.
Дисперсия – математическое ожидание квадрата отклонения случайной величины от квадрата ее математического ожидания.
В практике неизвестно МХ, поэтому:
![]() - смещенная характеристика поскольку
ее математическое ожидание
- смещенная характеристика поскольку
ее математическое ожидание
![]()
![]() -
несмещенная характеристика дисперсии.
-
несмещенная характеристика дисперсии.
Так как
среднее арифметическое
![]() вычисляется по результатам отдельных
наблюдений, то
является тоже случайной величиной и
характеризуется своим эмпирическим
средне квадратическим отклонением
вычисляется по результатам отдельных
наблюдений, то
является тоже случайной величиной и
характеризуется своим эмпирическим
средне квадратическим отклонением
![]()
![]()
Видно,
что эмпирическое среднее квадратическое
отклонение среднего арифметического
значения в
![]() раз меньше эмпирического среднего
квадратического отклонения, (т.е. точность
среднего арифметического значения в
раз выше точности единичного измерения).
Поэтому на практике за результат
измерения принимают
, а не результат отдельного измерения,
что позволяет уменьшить в
раз случайную составляющую погрешности
измерения.
раз меньше эмпирического среднего
квадратического отклонения, (т.е. точность
среднего арифметического значения в
раз выше точности единичного измерения).
Поэтому на практике за результат
измерения принимают
, а не результат отдельного измерения,
что позволяет уменьшить в
раз случайную составляющую погрешности
измерения.
Зная MX и G , можно с определенной вероятностью определить диапазон рассеивания результатов наблюдений .
![]()
где z - коэффициент равный значению функции Лапласа.
 68%
- доверительная вероятность
68%
- доверительная вероятность
В этом интервале лежат 68% всех размеров, среднеквадратическое отклонение является 68% или доверительным интервалом.
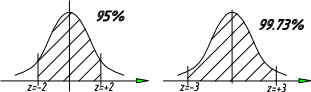
95% - в промышленности 99.73% - в научных исследованиях
Доверительный интервал, интервал в котором мы ожидаем размер.
Доверительная вероятность - вероятность того, что размеры деталей или результаты измерения окажется внутри доверительного интервала.
За оценку случайной погрешности результата измерений принимают доверительный интервал среднего арифметического.
Случайные погрешности, > 3G , считаются грубыми и исключаются из результата измерения.
При
малом n используют
коэффициент Стьюдента, где
![]()
При n распределение Стьюдента переходит в нормальное распределение, чем больше n, тем меньше коэф. Стьюдента, интервал с заданной вероятностью уменьшается
![]() ,
P= , n=
,
P= , n=
Систематическая погрешность.
![]()
Суммирование погрешностей.
1. Систематические погрешности суммируются алгебраически:
![]()
2. Случайные погрешности суммируются квадратически.
![]()
Погрешность косвенных измерений
![]()
![]()
![]()
![]()
L 3=
L1
–L2
3=
L1
–L2
![]()
![]()
![]()
![]()
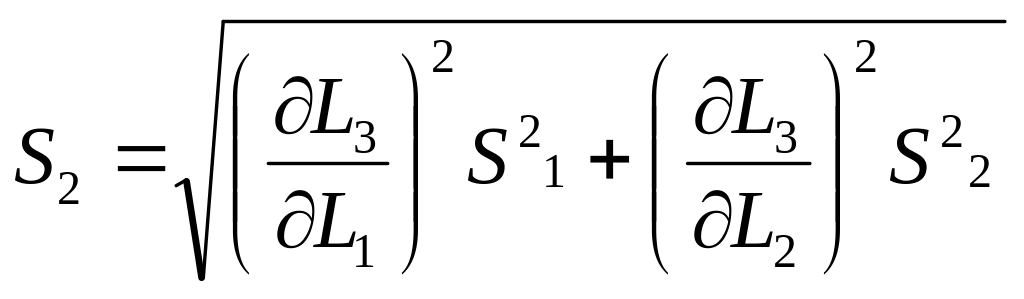
Выбор средства измерения по точности
Измерение
в сфере исследований ИЗМ=0,1R
Измерение
в сфере производства ДОПИЗМ=0,35-0.2T0,25Т![]()
ДОПСИ=0,7ДОПИЗМ

Выбирают в зависимости:
- от требований по точности измерения
- с учетом конструктивных особенностей, формы и размеров измеряемой детали
- экономичности
