Условие прочности при кручении вала

Условие прочности при кручении с учетом принятых обозначений формулируется следующим образом: максимальные касательные напряжения, возникающие в опасном сечении вала, не должны превышать допускаемых напряжений и записывается в виде

.

Как следует из закона парности касательных напряжений, одновременно с касательными напряжениями, действующими в плоскости поперечного сечения вала, имеют место касательные напряжения в продольных плоскостях. Они равны по величине парным напряжениям, но имеют противоположный знак. Таким образом, все элементы бруса при кручении находятся в состоянии чистого сдвига. Так как чистый сдвиг является частным случаем плоского напряженного состояния, при котором , , , то при повороте граней элемента на 45⁰в новых площадках обнаруживаются только нормальные напряжения, равные по величинеt(рис.5.7).

Рассмотрим возможные виды разрушения валов, изготовленных из различных материалов при кручении. Валы из пластичных материалов чаще всего разрушаются по сечению, перпендикулярному к оси вала, под действием касательных напряжений, действующих в этом сечении (рис.5.8а). Валы из хрупких материалов, разрушаются по винтовой поверхности наклоненной к оси вала под углом 45⁰, т.е. по направлению действия максимальных растягивающих напряжений (рис.5.8б). У деревянных валов первые трещины возникают по образующим цилиндра, так как древесина плохо сопротивляется действию касательных напряжений, направленных вдоль волокон (рис.5.8в).

Т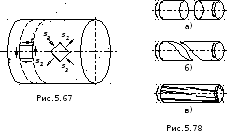аким образом, характер разрушения зависит от способности материала вала сопротивляться воздействию нормальных и касательных напряжений. В соответствии с этим, допускаемые касательные напряжения принимаются равным- для хрупких материалов и - для пластичных материалов.

Билет 7

 В предыдущем изложении методов расчета мы исходили из основного условия прочности . Это неравенство требует выбора размеров конструкции с таким расчетом, чтобы наибольшее напряжение в самом опасном месте не превосходило допускаемого.

   Но можно стать на другую точку зрения. Можно задать условие, чтобы действительная нагрузка на всю конструкцию не превосходила некоторой допускаемой величины. Условие это можно выразить таким неравенством:

   За допускаемую нагрузку надо выбрать некоторую часть той нагрузки, при которой конструкция перестанет функционировать правильно, перестанет выполнять свое назначение. Такая нагрузка обычно называется предельной, иногда—разрушающей в широком смысле слова (под разрушением конструкции подразумевают прекращение ее нормальной работы).

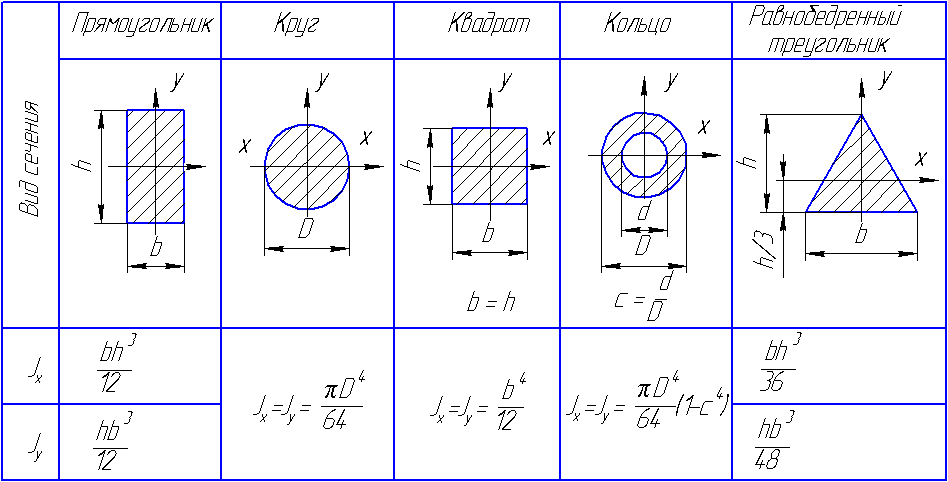
   В качестве примера возьмем систему из двух стальных стержней АВ и АС, (рис.2.9), нагруженных силой P.

Билет 8

Брус считается тонкостенным, если толщина стенки существенно меньше его прочих линейных размеров.

Линия, делящая толщину сечения пополам, называется средней линией или контуром сечения. Часто тонкостенное сечение, называемое также профилем, изображается только его средней линии, а размеры сечения задаются по этой линии.

Средняя линия может быть замкнутой и незамкнутой. Соответственно этому профили делятся на замкнутые и открытые.

При кручении тонкостенного бруса его поперечные сечения депланируют. Если ничто не препятствует свободной депланации сечений, кручение называется чистым или свободным. В противном случае кручение называется стесненным. При стесненном кручении, в отличие от свободного, в поперечных сечениях кроме касательных напряжений возникают также и нормальные напряжения.

Рассмотрим случай свободного кручения тонкостенного бруса замкнутого контура (рис. 7.10), при котором поперечные сечения могут свободно депланировать, но не искажаться в своей плоскости, т. е. не изменяется форма сечения в плане. Последнее условие обеспечивается в тонкостенных конструкциях установкой достаточно, жестких в своей плоскости диафрагм (в крыле самолета – нервюр, в фюзеляже - шпангоутов).

В случае кручения замкнутых тонкостенных профилей обычно считают, что толщина стенки настолько мала, что касательные напряжения по толщине стенки можно принять одинаковыми и равными напряжениям посредине толщины стенки и направленными по касательной к срединной линии толщины стенки. Составляя сумму проекций всех сил, приложенных к элементу, вырезанному из профиля (рис. 7.11), на ось профиля x, получим

2)

Билет 9

1)Универсальный метод определения перемещений (линейных и углов поворота) – метод Мора. К системе прикладывают единичную обобщенную силу в точке, для которой ищется обобщенное перемещение. Если определяется прогиб, то единичная сила представляет собой безразмерную сосредоточенную силу, если определяется угол поворота, то – безразмерный единичный момент. В случае пространственной системы действуют шесть компонентов внутренних усилий. Обобщенное перемещение определяется формулой (формула или интеграл Мора):

Ч

ерта над М,Q и N указывает на то, что эти внутренние усилия вызваны действием единичной силы. Для вычисления входящих в формулу интегралов надо перемножить эпюры соответствующих усилий. Порядок определения перемещения: 1) для заданной (действительной или грузовой) системы находят выражения M_n, N_n и Q_n; 2) по направлению искомого перемещения прикладывают соответствующую ему единичную силу (силу или момент); 3) определяют усилия от действия единичной силы; 4) найденные выражения подставляют в интеграл Мора и интегрируют по заданным участкам. Если полученное_mn>0, то перемещение совпадает с выбранным направлением единичной силы, если <0, то противоположно. Для плоской конструкции:

. Обычно при определении перемещений пренебрегают влиянием продольных деформаций и сдвигом, которые вызываются продольной N и поперечной Q силами, учитываются только перемещения, вызываемые изгибом. Для плоской системы будет: .

2)

Билет10

И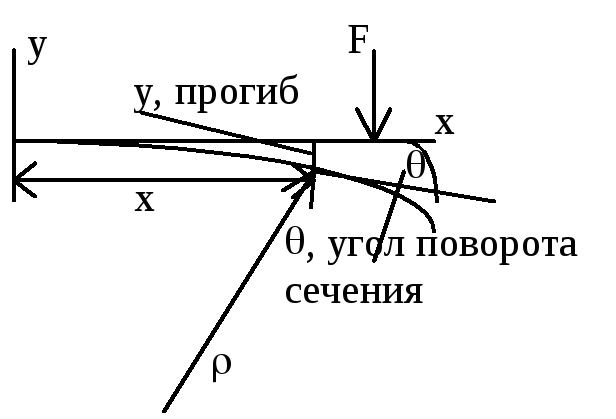меем закон Гука при изгибе:, где(х) — радиус кривизны изогнутой оси балки в сечении х, М(х) — изгибающий момент в том же сечении,EJ— жесткость балки. Из высшей математики известно: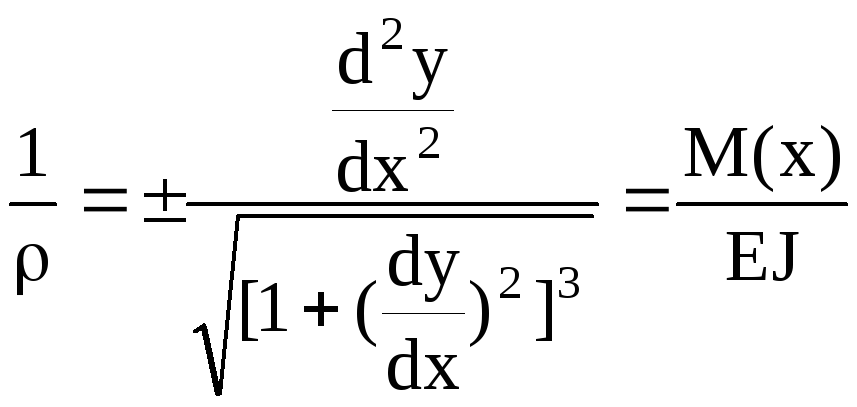— дифференциальное уравнение изогнутой оси балки.— тангенс угла между осью х и касательной к изогнутой оси. Эта величина очень мала (прогибы балки малы)ее квадратом пренебрегают и угол поворота сечения приравнивают тангенсу. Приближенноедифференциальное ур-ние изогнутой оси балки:. Если осьyнаправлена вверх, то знак (+). В некоторых вузах осьyнаправляется вниз(—). Интегрируя дифф. уравнение, получаем:—ур-ние углов поворота, интегрируем второй раз:— получаемур-ние прогибов. Постоянные интегрирования С иDнаходятся из граничных условий, которые зависят от способов закрепления балки.

2)Гука закон

основной закон, выражающий связь между напряжённым состоянием и деформацией упругого тела. Установлен англ. физиком Р. Гуком в 1660 для простейшего случая растяжения или сжатия стержня в форме: абсолютное удлинение (укорочение) Δl цилиндрического стержня прямо пропорционально растягивающей (сжимающей) силе N, т. е. Δl = kN, где k = l/ES /l — длина стержня, S — площадь его поперечного сечения, Е — модуль продольной упругости, являющийся механической характеристикой (константой) материала]. Г. з. удобно представлять также в форме σ= Еε, где σ= N/S — нормальное напряжение в поперечном сечении, ε = Δl/l — относительное удлинение (укорочение) стержня.

При сдвиге Г. з. записывается так: τ = G/γ, где τ — касательное напряжение, γ — сдвиг, G — т. н. модуль сдвига; при сдвиге касательное напряжение прямо пропорционально сдвигу.

Обобщённый Г. з. — для тела произвольной формы — утверждает, что 6 величин, определяющих напряжённое состояние в точке (см. Напряжение механическое), выражаются линейно через 6 величин, определяющих деформацию (См. Деформация) в окрестности рассматриваемой точки. Коэффициент пропорциональности в этих соотношениях называются модулями упругости (См. Модули упругости). В анизотропных телах, например в кристаллах, модули упругости различны в разных направлениях, поэтому в общем случае упругие свойства твёрдого тела характеризуются с помощью 21 модуля упругости. Для изотропных тел число независимых упругих постоянных сводится к двум (см. Ламе постоянные).

Г. з. не имеет места, когда некоторые напряжения (или деформации) достигают предельных значений, характерных для каждого материала, и тело переходит в упруго-пластическое состояние. Г. з. является основным соотношением, применяемым при расчёте на прочность и деформируемость конструкций и сооружений.

Билет 11

2)Для построения теории сопротивления материалов принимают ряд гипотез о структуре и свойствах материалов, а также о характере деформации.

1. Гипотеза о сплошности материала. Предполагается, что материал полностью заполняет занимаемый им объем. Атомистическая теория дискретного строения вещества во внимание не принимается.

2. Гипотеза об однородности и изотропности. Предполагается, что свойства материала одинаковы во всех точках и в каждой точке — во всех направлениях. В некоторых случаях предположение об изотропии материала неприемлемо. Так, анизотропными являются древесина, свойства которой вдоль и поперек волокон существенно различны, а также армированные материалы или так называемые композиционные материалы.

3. Гипотеза о малости деформации (гипотеза относительной жесткости материала). Предполагается, что деформации малы по сравнению с размерами деформируемого тела. На этом основании пренебрегают изменениями в расположении внешних сил относительно отдельных частей тела при деформации и уравнения статики составляют для недеформированного тела. В некоторых случаях от этого принципа приходится отступать, что оговаривается особо.

4. Гипотеза о совершенной упругости материала. Все тела предполагаются абсолютно упругими. В действительности реальные тела можно считать упругими только до определенных величин нагрузок, и это необходимо учитывать, применяя формулы сопротивления материалов,

5. Гипотеза о линейной зависимости между деформациями и нагрузками. Предполагается, что для большинства материалов справедлив закон Гука, устанавливающий прямо пропорциональную зависимость между деформациями и нагрузками.

Как следствие гипотез о малости деформаций и о линейной зависимости между деформациями и усилиями при решении большинства задач сопротивления материалов применим принцип суперпозиции (принцип независимости действия и сложения сил). Например, усилия в любом элементе конструкции, вызванные различными факторами (несколькими силами, температурными воздействиями), равны сумме усилив, вызванных каждым из этих факторов, и не зависят от порядка их приложения. Это же справедливо и в отношении деформаций.

6. Гипотеза плоских сечений. Предполагается, что мысленно проведенные плоские сечения, перпендикулярные к оси стержня, в процессе его деформирования остаются плоскими и перпендикулярными к оси.

Эти, а также некоторые другие гипотезы позволяют решать широкий круг задач по расчету на прочность, жесткость и устойчивость, результаты таких расчетов обычно хорошо согласуются с данными эксперимента.

Билет 12