
- •Содержание
- •Глава 5. Алгоритмы сортировок 52
- •Глава 6. Алгоритмы поиска 63
- •Глава 1. Основные операции при работе с деревьями
- •1.1. Определение глубины дерева
- •1.2. Операции поиска и включения элемента в дерево
- •1.3. Оптимизация поиска в дереве
- •1.3.1. Обходы дерева с нумерацией вершин
- •1.4. Поиск и включение в двоичное дерево
- •Контрольные вопросы
- •Задания для практической работы
- •Глава 2. Сбалансированные двоичные деревья
- •2.1. Преобразование двоичного дерева в лозу.
- •2.2. Преобразование лозы в сбалансированное двоичное дерево.
- •Контрольные вопросы
- •Задания для практической работы
- •Глава 3. Жадные алгоритмы
- •3.1. Понятие жадного алгоритма
- •3.2. Алгоритм Хаффмана
- •Контрольные вопросы
- •Задания для практической работы
- •Глава 4. Графы
- •4.1. Алгоритмы представления графа
- •4.1.1. Представление графа в виде массива
- •4.1.2. Представление графа в виде матрицы смежности
- •4.1.3. Представление графа в виде связанного списка
- •4.1.4. Представление графа в виде списка дуг
- •4.1.5. Преобразования структур графа
- •4.2. Обходы в графах
- •4.3. Определение путей и контуров Эйлера
- •4.4. Поиск кратчайших путей
- •4.4.1. Алгоритм э. Дейкстры.
- •4.4.2. Алгоритм Флойда — Уоршалла
- •4.5. Определение остовных деревьев
- •4.5.1. Алгоритм Крускала
- •4.5.2. Алгоритм Прима
- •Контрольные вопросы
- •Определение путей и контуров Эйлера
- •Задания для практической работы
- •Глава 5. Алгоритмы сортировок
- •5.1. Сортировка выбором
- •5.2. Сортировка вставками
- •5.3. Пузырьковая сортировка
- •5.4. Быстрая сортировка
- •5.5. Сортировка слиянием
- •5.6. Пирамидальная сортировка
- •Контрольные вопросы
- •Задания для практической работы
- •Глава 6. Алгоритмы поиска
- •6.1. Последовательный поиск
- •6.2. Двоичный поиск
- •6.3. Работа со словарем. Иоиск и вставка. Хеширование.
- •6.4. Поиск подстроки в строке
- •6.4.1. Алгоритм прямого поиска подстроки в строке
- •Контрольные вопросы
- •Задания для практической работы
- •Литература
Содержание
Глава 1. Основные операции при работе с деревьями 4
1.1. Определение глубины дерева 5
1.2. Операции поиска и включения элемента в дерево 5
1.3. Оптимизация поиска в дереве 6
1.3.1. Обходы дерева с нумерацией вершин 7
1.4. Поиск и включение в двоичное дерево 8
Контрольные вопросы 9
Задания для практической работы 9
Глава 2. Сбалансированные двоичные деревья 14
2.1. Преобразование двоичного дерева в лозу. 14
2.2. Преобразование лозы в сбалансированное двоичное дерево. 15
Контрольные вопросы 17
Задания для практической работы 17
Глава 3. Жадные алгоритмы 18
3.1. Понятие жадного алгоритма 18
3.2. Алгоритм Хаффмана 18
Контрольные вопросы 20
Задания для практической работы 21
Глава 4. Графы 22
4.1. Алгоритмы представления графа 22
4.1.1. Представление графа в виде массива 23
4.1.2. Представление графа в виде матрицы смежности 24
4.1.3. Представление графа в виде связанного списка 26
4.1.4. Представление графа в виде списка дуг 29
4.1.5. Преобразования структур графа 31
4.2. Обходы в графах 32
4.3. Определение путей и контуров Эйлера 35
4.4. Поиск кратчайших путей 37
4.4.1. Алгоритм Э. Дейкстры. 38
4.4.2. Алгоритм Флойда — Уоршалла 40
4.5. Определение остовных деревьев 41
4.5.1. Алгоритм Крускала 42
4.5.2. Алгоритм Прима 46
Контрольные вопросы 49
Задания для практической работы 49
Глава 5. Алгоритмы сортировок 52
5.1. Сортировка выбором 52
5.2. Сортировка вставками 52
5.3. Пузырьковая сортировка 53
5.4. Быстрая сортировка 54
5.5. Сортировка слиянием 55
5.6. Пирамидальная сортировка 57
Контрольные вопросы 61
Задания для практической работы 61
Глава 6. Алгоритмы поиска 63
6.1. Последовательный поиск 63
6.2. Двоичный поиск 63
6.3. Работа со словарем. Иоиск и вставка. Хеширование. 63
6.4. Поиск подстроки в строке 70
6.4.1. Алгоритм прямого поиска подстроки в строке 70
6.4.2. БМ-поиск (Боуера–Мура) 72
6.4.3. КМП-поиск (Кнута–Мориса и–Пратта) 75
Контрольные вопросы 80
Задания для практической работы 81
Литература 82
Глава 1. Основные операции при работе с деревьями
К основным операциям работы с деревьями относятся:
а) поиск элемента в дереве. Операция заключается в прохождении узлов дерева в одном из рассмотренных выше порядке. При прохождении дерева поиска достаточно пройти только то поддерево, которое возможно содержит искомый элемент;
б) включение элемента в дерево. Операция заключается в добавлении листа (исключая сбалансированное дерево – включение элемента в сбалансированное дерево приводит, как правило, к его перестройке) в какое-то поддерево, если такого элемента нет в исходном дереве. При включении нового элемента в дерево поиска лист добавляется в то поддерево, в котором не нарушается отношение порядка;
в) удаление элемента из дерева. Операция заключается в изменении связей между дочерними и родительскими, по отношению к удаляемому, элементами (исключая сбалансированное дерево – удаление элемента из сбалансированного дерева приводит, как правило, к его перестройке); здесь необходимо рассматривать три случая: удаление листа (см. рис.1.а), удаление элемента с одним потомком (см. рис.1.б), удаление элемента с двумя потомками (см. рис.1.в).
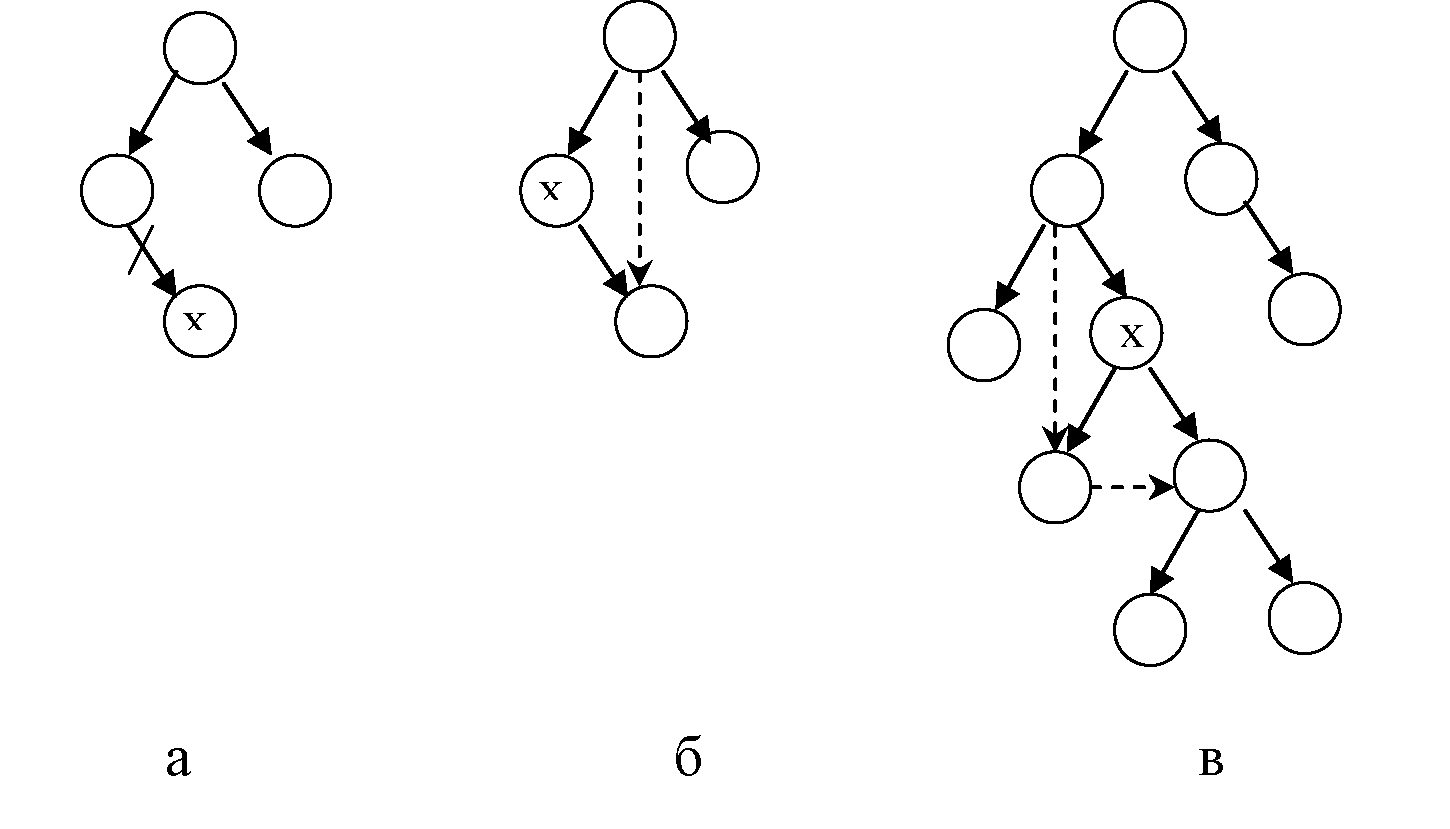
Рис. 1. Случаи удаления листа дерева
При удалении элемента степени 2 из дерева поиска изменять связи необходимо так, чтобы не нарушалось установленное в дереве отношение порядка. Лучшим вариантом в этом случае будет перемещение на место удаляемого элемента либо самого правого листа из левого поддерева удаляемого элемента, либо самого левого листа из правого поддерева удаляемого элемента;
г) сравнение деревьев (проверка деревьев на равенство). Операция заключается в прохождении обоих деревьев в одном порядке до тех пор, пока либо не будут пройдены оба дерева, либо одно из них, либо соответствующие элементы окажутся не равными, либо в одном из деревьев не будет обнаружено отсутствие соответствующего элемента. Только в случае равенства деревьев оба дерева будут пройдены одновременно;
д) копирование дерева. Операция заключается в прохождении исходного дерева и построении нового дерева с элементами, информационные поля которых равны информационным полям соответствующих элементов исходного дерева.
Далее рассмотрим операции поиска и включения элемента в дерево. Остальные операции можно выполнить на основе работы алгоритмов поиска и включения элемента в дерево.
