5.3. Ускорение точки

Ускорение точки характеризует быстроту изменения вектора скорости в данный момент времени как по модулю, так и по направлению.

Рассмотрим векторный способ задания движения точки. Пусть точка , движущаяся относительно неподвижной системы отсчета, в момент времени занимает положение , а в момент – положение ; скорости точки в этих положениях представлены векторами и (рис. 3).

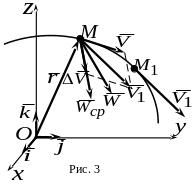Перенесем начало вектора в точку и построим параллелограмм, в котором диагональю будет , а одной из сторон – вектор . Другая сторона будет изображать вектор , т. е. приращение вектора за время . Векторная величина 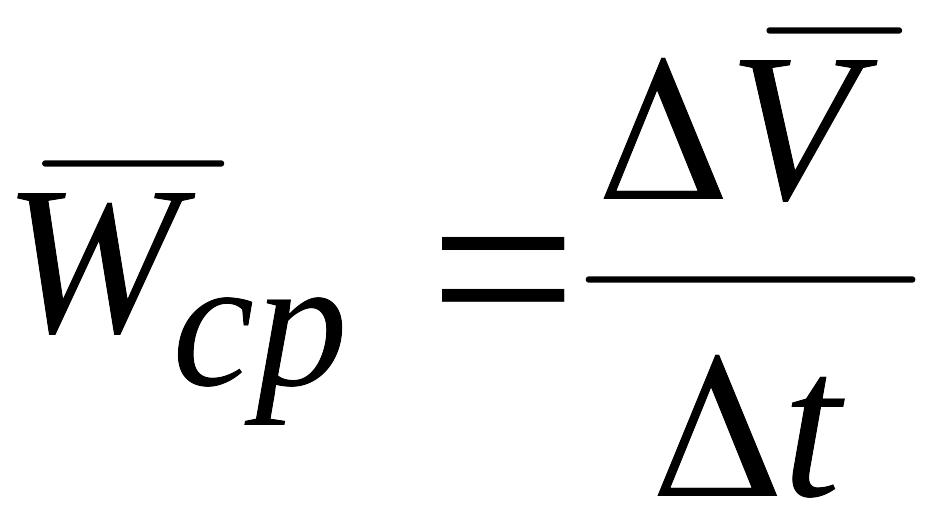называется средним ускорением точки за время , вектор направлен так же, как и вектор .

Ускорением точки в данный момент времени называется вектор , равный пределу, к которому стремится при .

. (16)

Учитывая формулу (6), можно записать

. (17)

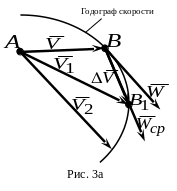Ускорение точки в данный момент времени равно первой производной по времени от вектора скорости точки или второй производной по времени от радиус-вектора точки.

Проведем из какой-либо неподвижной точки векторы , в моменты времени (рис. 3а). Геометрическое место концов этих векторов представляет годограф вектора скорости точки. Среднее ускорение за время направлено по хорде годографа, а ускорение в данный момент времени параллельно касательной к годографу скорости в точке .

Пусть движение точки задается уравнениями (2), то есть координатным способом. Формулу (16) с учетом зависимости (9) можно представить в следующем виде:

. (18)

С другой стороны

(19),

где – проекции вектора ускорения точки на оси координат. Сравнивая (18) и (19) находим

. (20)

Но .

Поэтому получим

. (21)

Следовательно, проекции вектора ускорения точки на неподвижные оси декартовых координат равны первым производным по времени от соответствующих проекций скоростей или вторым производным по времени от соответствующих координат.

Модуль ускорения точки равен

, (22)

а направление вектора точки определяется следующими направляющими косинусами:

. (23)

5.4. Естественные оси

Дальнейшее изучение ускорения точки предполагает введение понятия об естественных осях. Рассмотрим точку , которая движется по траектории, представляющей собой пространственную кривую (рис 4). Выберем на ней начало и положительное направление отсчета дуговой координаты . Выберем также вблизи точки некоторую точку и проведем через них касательные к кривой и . Обозначим орты касательных в этих точках соответственно и . Перенесем орт в точку и проведем через орты и плоскость . При неограниченном приближении точки к точке , вследствие изменения положения орта плоскость будет поворачиваться вокруг касательной, проходящей через точку , приближаясь к некоторой плоскости . Эта плоскость, представляющая собой предельное положение плоскости , называется соприкасающейся плоскостью данной кривой в точке .

Плоскость (рис 5.), проведенная через точку перпендикулярно касательной в этой точке называется нормальной плоскостью. Любая прямая, переходящая через точку и лежащая в этой плоскости является нормалью кривой в точке . Нормаль , расположенная в соприкасающейся плоскости, называется главной нормалью. Положительное направление главной нормали определяется ортом главной нормали , направленным в сторону вогнутости кривой.

Н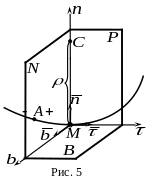 ормаль , перпендикулярная соприкасающейся плоскости, называется бинормалью к кривой в точке . Положительное направление бинормали определяется ее ортом , причем , т.е. орты ориентированы друг относительно друга так же, как орты правой прямоугольной декартовой системы координат.

Плоскость , проходящая через касательную и бинормаль, называется спрямляющей.

Отметим, что для плоской траектории соприкасающейся будет плоскость, в которой лежит кривая, а главной нормалью будет нормаль, проведенная в точке в этой плоскости в сторону вогнутости кривой.

Три взаимно перпендикулярные оси: касательная , главная нормаль и бинормаль образуют естественные оси кривой в данной точке. Двигаясь по кривой вместе с точкой естественные оси, оставаясь ортогональными, изменяют свою ориентацию в пространстве относительно неподвижной системы отсчета .