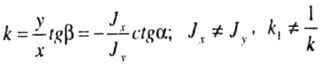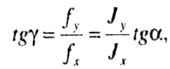1) Косой изгиб. Определение напряжений

КОСОЙ ИЗГИБ

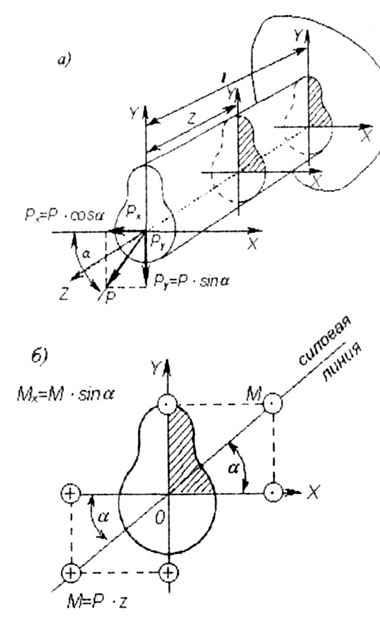
Косым изгибом называется такой вид изгиба, при котором плоскость нагрузки (силовая линия) изгибающего момента не совпадает ни с одной из главных осей инерции поперечного сечения стержня X, Y (рис. 7.1, а, б).

При косом изгибе действующие внешние силы (моменты) представляют их проекциями на главные оси поперечного сечения (рис. 7.1, б), тем самым сводят задачу к случаю поперечного изгиба в двух главных плоскостях. Из рис. 7.1, а, б видно, что:

Изгибающие моменты в расчетном сечении:

При выбранном направлении главных центральных осей инерции положительным октантом будет первый октант (на рис. 7.1, а, б заштрихован).

Рис. 7.1

Правило знаков. Изгибающие моменты в расчетном поперечном сечении считаются положительными, если они вызывают в первом (заштрихованном) октанте напряжения растяжения.

Нормальные напряжения в точках поперечного сечения с текущими координатами х, у определяются алгебраической суммой напряжений, вызываемых изгибающими моментами М_xи М_y:

где J_xи J_y— моменты инерции поперечного сечения относительно главных, центральных осей инерции сечения X, Y, т. е. изменяются по линейному закону. Уравнение нейтральной (нулевой) линии в сечении найдем, приравняв

Ответы совпали.

При х = 0 значение у = 0, т. е. прямая с угловым коэффициентом k проходит через центр тяжести поперечного сечения.

При косом изгибе нейтральная линия представляет собой прямую, которая не перпендикулярна к плоскости изгибающего момента , или, что одно и то же, к силовой линии.

Силовая линия наклонена к оси X под углом а, следовательно, ее угловой коэффициент равен:

Угловой коэффициент нейтральной линии:

Так как в общем случае J_xне равно J_y, то и k₁не равно — 1/k, следовательно, нулевая длина не перпендикулярна силовой линии, а повернута в сторону главной оси минимального момента инерции.

Нейтральная линия разделяет поперечное сечение на две зоны:

• в которой действуют только напряжения растяжения;

• в которой действуют только напряжения сжатия. Первый (заштрихованный) квадрант (рис 7.1, а) находится всегда в зоне действия напряжений растяжения. Максимальные по величине нормальные напряжения находятся в точках поперечного сечения максимально удаленных от нейтральной оси.

Максимальные по величине напряжения растяжения возникают в точке А с координатами X_a, Y_л, а максимальные напряжения сжатия возникают в точке В с координатами X_В, Y_В(рис. 7.1, в):

Получим эпюру нормальных напряжений в расчетном сечении (7.1, в).

Условие прочности. Если материал стержня одинаково работает на растяжение и на сжатие, то условие прочности записывается в виде:

Если материал стержня работает на растяжение и на сжатие не одинаково, то расчет проводится раздельно, т. е. проверяются условия прочности:

Для поперечных сечений, имеющих две оси симметрии:

где W_x, W_y— момент сопротивления поперечного сечения относительно главных, центральных осей инерции X, Y.

Прогибы при косом изгибе. Прогиб конца консоли от действия Р_xнаправлен по оси X и равен:

Прогиб от действия Р_yнаправлен по оси Y и равен:

Модуль полного прогиба конца консоли

Угол наклона вектора f к оси X

т. е. угловой коэффициент

перемножив k на k₂получим:

что свидетельствует о том, что нулевая линия и направление полного прогиба взаимно