
- •Поле комплексных чисел
- •Сопряжение комплексных чисел
- •Тригонометрическая форма записи комплексных чисел
- •Комплексная экспонента
- •Извлечение корней из комплексных чисел.
- •Последовательности и ряды комплексных чисел
- •Расширенная комплексная плоскость
- •Дробно-линейная функция
- •Группа дробно-линейных преобразований сферы Римана
- •Инверсия.
- •Аналитичность
- •Гармонические функции
- •Степенные ряды
- •Основные функции комплексной переменной
- •Экспонента
- •Тригонометрические и гиперболические функции
- •Аргумент комплексного числа
- •Многозначные функции
- •Интегрирование функции комплексного переменного
- •Кривые на комплексной плоскости
- •Определение и свойства интеграла
- •Длина кривой
- •Теорема Коши
- •Теорема Коши для односвязной области
- •Распространение на многосвязные области
- •Интегральная формула Коши
- •Ряд Тейлора
- •Теорема единственности и аналитическое продолжение
- •Ряд Лорана
- •Изолированные особые точки
- •1. Особые точки
- •2. Разложение в окрестности особой точки
- •Основная теорема о вычетах
- •Вычисление интегралов с помощью вычетов
- •Литература
Аргумент комплексного числа
Главным значением аргумента ненулевого комплексного числа z назовем то единственное действительное число 𝜑 ∈ [0,2π ), для которого z /| z| =exp(i𝜑 ). Обозначаем главное значение аргумента как arg z.
Всевозможные
решения уравнения
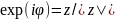 относительно переменной 𝜑,
т.е. множество {arg z+2π k ∣
k∈ ℤ
} назовем аргументом комплексного
числа z и обозначим Arg z. Таким образом
Arg z -- многозначная функция.
относительно переменной 𝜑,
т.е. множество {arg z+2π k ∣
k∈ ℤ
} назовем аргументом комплексного
числа z и обозначим Arg z. Таким образом
Arg z -- многозначная функция.
Многозначные функции
Примерами
многозначных функций являются аргумент
Arg z и
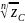 . Ветвью многозначной функции
. Ветвью многозначной функции
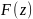 в области D назовем такую
непрерывную однозначную функцию
,
что
в области D назовем такую
непрерывную однозначную функцию
,
что
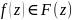 для любого
для любого
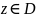 .
Для некоторых областей D⊆
ℂ можно выделить
ветвь многозначной функции с соблюдением
непрерывности или аналитичности, а для
других нет. Так например, для области
.
Для некоторых областей D⊆
ℂ можно выделить
ветвь многозначной функции с соблюдением
непрерывности или аналитичности, а для
других нет. Так например, для области
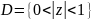 и функции
и функции
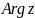 нельзя выделить ветвь, а для области
нельзя выделить ветвь, а для области

0 1
-1
Рис. Выделение ветви функции Arg z
можно: пусть
ψ (z)=arg z+2πkz, где kz -- целое
число, которое указано на рисунке в той
части области D, в которой лежит комплексное
число z. Если z лежит на границе, то берется
любое из двух возможных целых чисел.
Построенная таким образом ветвь будет
непрерывной функцией. Теперь можно
построить и аналитическую ветвь
многозначной функции и
в той же области D --
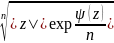 . Заметим, что для кольца 0<|z| <R такое
построение, с соблюдением аналитичности,
невозможно.
. Заметим, что для кольца 0<|z| <R такое
построение, с соблюдением аналитичности,
невозможно.
Определим
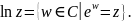
Если z=x -- положительное действительное число, то в силу монотонности действительной функции ey, существует только одно действительное число в множестве Ln x. Оно есть не что иное как натуральный логарифм числа x (обозначается ln x).
Предложение.
Пусть
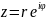 -- показательная форма записи. Тогда
-- показательная форма записи. Тогда
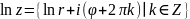
Пример. Вычислим:
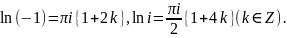
Свойства комплексного логарифма таковы.
Л1. Область допустимых значений логарифма -- все ненулевые комплексные числа. Если z=rei𝜑 , где r=|z| и 𝜑 ∈ Arg z, то Ln z={ln r+i(𝜑 +2π k) | k∈ ℤ } .
Л2 [производная логарифма] (Ln z)'= 1 / z . (Имеется в виду производная от любой ветви логарифма)
Доказательство. Дифференцируем левую и правую часть соотношения ew=z, считая w функцией от z. Получаем: ew⋅ w'z=1, откуда w'z= 1/ew =1/z .
Следующее свойство вытекает из основного функционального соотношения для экспоненты.
Л3. Для любых ненулевых комплексных чисел z1, z2 и z выполняются равенства:
Ln(z1⋅ z2)=Ln z1+Ln z2; Ln zk=k Ln z (k∈ ℤ ).
С помощью комплексного логарифма можно определить степень любого ненулевого комплексного числа с любым комплексным показателем:
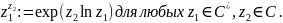
Пример ii={e-π /2-2πk | k∈ ℤ } .
Л4. Для всех ненулевых комплексных чисел имеет место равенство:
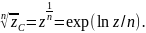
Определим теперь обратные тригонометрические и обратные гиперболические функции:
Arcsin z={ w∈ ℂ | sin w=z} ; Arccos z={ w∈ ℂ | cos w=z} ;
Arcsh z={ w∈ ℂ | sh w=z} ; Arcch z={ w∈ ℂ | ch w=z };
Arctg z={ w∈ ℂ | tg w=z} ; Arcth z={ w∈ ℂ | th w=z} .
Используя
комплексный логарифм, установим формулы
для вычислений этих многозначных
функций. Начнем с решения уравнения ch
w=z относительно w. Заменяя ζ =ew,
сводим это уравнение к квадратному
ζ2-2zζ +1=0, решения которого суть:
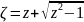 . Получаем окончательно:
. Получаем окончательно:
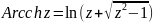 .
.
Аналогично:
Arccos z=-i Ln(z+√(z2-1)); Arcsh z=Ln(z+√(z2+1) ); Arcsin z=- i Ln(iz+√(1-z2));
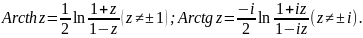
Пример
Вычислим:
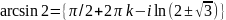 ;
;
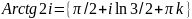 .
.
