
- •Поле комплексных чисел
- •Сопряжение комплексных чисел
- •Тригонометрическая форма записи комплексных чисел
- •Комплексная экспонента
- •Извлечение корней из комплексных чисел.
- •Последовательности и ряды комплексных чисел
- •Расширенная комплексная плоскость
- •Дробно-линейная функция
- •Группа дробно-линейных преобразований сферы Римана
- •Инверсия.
- •Аналитичность
- •Гармонические функции
- •Степенные ряды
- •Основные функции комплексной переменной
- •Экспонента
- •Тригонометрические и гиперболические функции
- •Аргумент комплексного числа
- •Многозначные функции
- •Интегрирование функции комплексного переменного
- •Кривые на комплексной плоскости
- •Определение и свойства интеграла
- •Длина кривой
- •Теорема Коши
- •Теорема Коши для односвязной области
- •Распространение на многосвязные области
- •Интегральная формула Коши
- •Ряд Тейлора
- •Теорема единственности и аналитическое продолжение
- •Ряд Лорана
- •Изолированные особые точки
- •1. Особые точки
- •2. Разложение в окрестности особой точки
- •Основная теорема о вычетах
- •Вычисление интегралов с помощью вычетов
- •Литература
Степенные ряды
Пусть
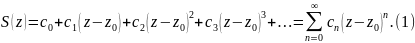
Через R
обозначим радиус сходимости ряда (1).
Тем самым ряд (1) равномерно сходится к
 в любом замкнутом круге
в любом замкнутом круге
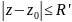 при условии
при условии
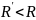 .
В частности
.
В частности
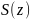 будет непрерывной функцией на открытом
круге
будет непрерывной функцией на открытом
круге
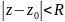 .
.
Теорема. Функция S(z) аналитична в круге сходимости и
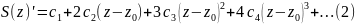
При этом ряд в правой части (2) имеет тот же радиус сходимости, что и ряд (1).
Далее будут рассматриваться также и ряды вида
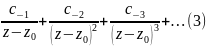
Такие ряды
заменой
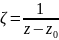 сводятся к степенным рядам по степеням
ζ . Из теоремы Абеля вытекает:
сводятся к степенным рядам по степеням
ζ . Из теоремы Абеля вытекает:
Следствие. Существует неотрицательное действительное число r или +∞ такое, что ряд (3) сходится абсолютно в области |z-z0| >r, и его сумма -- аналитическая в это
Пример.
Ряд
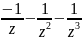 -....
сходится в области
-....
сходится в области
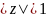 ,
и его сумма совпадает в этой области
с функцией
,
и его сумма совпадает в этой области
с функцией
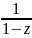 .
.
Основные функции комплексной переменной
Экспонента
Напомним
определение комплексной экспоненты –
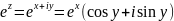 .
Тогда
.
Тогда
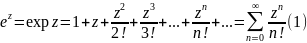
-- разложение в ряд Маклорена. Радиус сходимости этого ряда равен +∞, значит комплексная экспонента аналитична на всей комплексной плоскости и
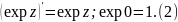
Первое равенство здесь следует, например, из теоремы о почленном дифференцировании степенного ряда.
Тригонометрические и гиперболические функции
Синусом комплексного переменного называется функция
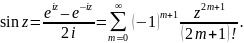
Косинус комплексного переменного есть функция
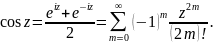
Гиперболический синус комплексного переменного определяется так:
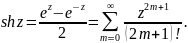
Гиперболический косинус комплексного переменного -- это функция
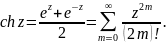
Отметим некоторые свойства вновь введеных функций.
A. Если x∈ ℝ , то cos x, sin x, ch x, sh x∈ ℝ .
Б. Имеет место следующая связь тригонометрических и гиперболических функций:
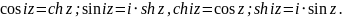
В. Основные тригонометрическое и гиперболическое тождества:
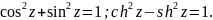
Доказательство основного гиперболического тождества:
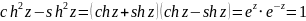
Доказательство основного тригонометрического тождества:
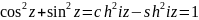
(применено свойство Б)
Г Формулы сложения:
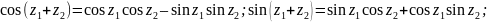
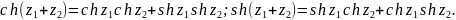
В частности,


Д. Для вычисления производных тригонометрических и гиперболических функций следует применить теорему о почленном дифференцировании степенного ряда. Получим:
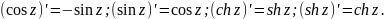
Е. Функции cos z, ch z четны, а функции sin z, sh z нечетны.
Ж. (Периодичность) Функция ez периодична с периодом 2π i. Функции cos z, sin z периодичны с периодом 2π , а функции ch z, sh z периодичны с периодом 2πi. Более того,
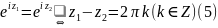
Применяя формулы суммы, получаем разложение на действительную и мнимую части экспоненты и тригонометрических, а также гиперболических функций.
З. Разложения на действительную и мнимую части:
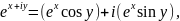
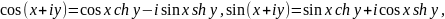
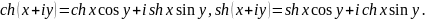
Если однозначная аналитическая функция отображает биективно область D на область G, то D называется областью однолистности.
И. Область
Dk={ x+iy | 2π k≤ y<2π (k+1)} для любого
целого k является областью однолистности
функции ez, которая отображает ее
на область
 .
.
Доказательство. Из соотношения (5) следует инъективность отображения exp:Dk→ ℂ . Пусть w -- любое ненулевое комплексное число. Тогда, решая уравнения ex=|w| и eiy =w/|w| с действительными переменными x и y (y выбираем из полуинтеравала [2πk, 2π (k+1))), получим z=x+iy∈Dk такое, что exp z=w. Сюръективность доказана.
Следствием предыдущего свойства является
К. Область значений. Область значений функций cos z, sin z, ch z, sh z есть все поле комплексных чисел.
Л. Нули Решением уравнения sin z=0 является множество {πk | k∈ ℤ } . Нули функции cos z -- множество { π /2+πk | k∈ ℤ } . Нулями функции sh z является множество { πki | k∈ ℤ} , а нули функции ch z -- множество { π/2i+πki | k∈ ℤ } .
Доказательство. Имеет место соотношения sin z=0 тогда и только тогда, когда eiz -e-iz =0 Это равносильно соотношению e2iz =0, что дает 2iz=2πik. Окончательно, z=2πk (k∈ ℤ ). Аналогично доказываются утверждения для остальных функций.□
Функция tg z=sin z /cos z называется тангенсом, а функция th z= sh z/ ch z называется гиперболическим тангенсом. Производные тангенсов вычисляются c использованием известного правила "производная отношения":
(tg z)'=1/cos2z , (th z)'= 1/ch2z .
Область допустимых значений тангенса tg z есть многосвязная область ℂ \{π /2+πk | k∈ ℤ }
