8. Аналитичность

Пусть функция f(z) определена в окрестности точки z₀. Производная функции комплексного переменного w=f(z) в точке z₀ определяется в точности также как и для функции действительного переменного.

Функция комплексного переменного называется аналитической в точке, если она имеет производную в некоторой окрестности этой точки. Аналитичность на замкнутой области D означает существование производной на некоторой открытой области G, содержащей D.

Имеют место обычные правила дифференцирования: производная суммы, произведения, частного и производная сложной функции. Производная постоянной функции равна 0. Если w=f(z) и z=g(w) -- две взаимно-обратные функции, то g'(w)= 1 / f'(z) .

Многочлен w=c₀+c₁z+… +c_nzⁿ является аналитической функцией на всей комплексной плоскости. Дробно-линейная функция аналитична всюду, кроме точки -d/c (при c≠ 0), при этом ее производная w'= (ad-dc) / (cz+d)² нигде не обращается в ноль.

Пример. Функция 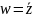не аналитична ни в одной точке, так как отношение 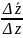стремиться к 1, если 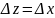и стремитькся к -1, если .

Предложение. Из аналитичности функции следует ее непрерывность.

Условия Коши-Римана. Если функция f(z)=u(x,y)+iv(x,y) аналитична в точке z₀, то выполнены условия

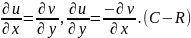
Наоборот, если в открытой области существут и непрерывны все четыре частные производные 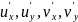и при этом выполнено в этой области условие (C-R), то функция 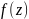аналитична.

Доказательство. Если f(z) аналитична, то рассмотрев два случая Δz=Δx и Δz=iΔy, получаем следующие значения производной: f'(z)=∂u/∂x+i∂v/∂x и f'(z)=-i∂u/∂y+∂v/∂y. Приравнивая действительные и мнимые части в равенстве ∂u/∂x+i∂v/∂x = -i∂u/∂y+∂v/∂y, получаем условия Коши-Римана.

Наоборот, если условия Коши-Римана выполнены и частные производные непрерывны, то, учитывая дифференцируемость функций u и v, выводим:

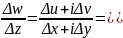
для некоторой б.м. α . Устремляя Δz к нулю, получаем, что производная w'_z существует и равна u'_x+iv'_x. □

9. Гармонические функции

Дифференциальный оператор Δ =∂²/∂x² + ∂² / ∂y² называется оператором Лапласа, а решения дифференциального уравнения Лапласа

∂²u / ∂x² + ∂²u/∂y² =0

называют гармоническими функциями. Например, все линейные функции 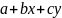гармоничны. Квадратичная форма 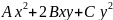гармонична тогда и только тогда, когда 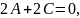т.е. .

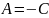Сформулируем две физические задачи, для которых математической моделью является уравнение Лапласа.

А. Пусть D -- физическая однородная пластинка, одинаковой толщины, теплоизолированная снизу и сверху. Обозначим через u(x,y) температуру в точке (x,y)∈ D. Полагаем, что температура на границе пластинки ∂D нам известна и поддерживается так, что она не зависит от времени. Тогда u(x,y) -- гармоническая функция, т. е. u(x,y) -- решение уравнения Лапласа с граничным условием, заданным распределением температуры на границе пластинки.

Б. Пусть Γ -- проволочный каркас, помещенный в пространство Oxyu так, что кривая Γ есть график функции u(x,y), (x,y)∈ L, а L -- замкнутая гладкая кривая в плоскости Oxy (как, например, окружность), ограничивающая область D. Натянем на проволочный каркас мыльную пленку, и пусть функция u(x,y), (x,y)∈ D описывает вид этой мыльной пленки. Иными словами, мыльная пленка есть график функции u(x,y) с областью определения D. Тогда u(x,y) -- гармоническая функция.

Предложение. Если f(z)=u+iv -- аналитическая функция, то u и v -- гармонические функции.

Доказательство. Имеем:

∂²u/∂x² + ∂²u/∂y² =

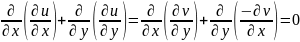
Аналогично доказывается, что v -- гармоническая функция.

Более точно, функции u(x,y) и v(x,y) называются сопряженными гармоническими функциями.

В полярных координатах оператор Лапласа имеет вид