
- •Поле комплексных чисел
- •Сопряжение комплексных чисел
- •Тригонометрическая форма записи комплексных чисел
- •Комплексная экспонента
- •Извлечение корней из комплексных чисел.
- •Последовательности и ряды комплексных чисел
- •Расширенная комплексная плоскость
- •Дробно-линейная функция
- •Группа дробно-линейных преобразований сферы Римана
- •Инверсия.
- •Аналитичность
- •Гармонические функции
- •Степенные ряды
- •Основные функции комплексной переменной
- •Экспонента
- •Тригонометрические и гиперболические функции
- •Аргумент комплексного числа
- •Многозначные функции
- •Интегрирование функции комплексного переменного
- •Кривые на комплексной плоскости
- •Определение и свойства интеграла
- •Длина кривой
- •Теорема Коши
- •Теорема Коши для односвязной области
- •Распространение на многосвязные области
- •Интегральная формула Коши
- •Ряд Тейлора
- •Теорема единственности и аналитическое продолжение
- •Ряд Лорана
- •Изолированные особые точки
- •1. Особые точки
- •2. Разложение в окрестности особой точки
- •Основная теорема о вычетах
- •Вычисление интегралов с помощью вычетов
- •Литература
Извлечение корней из комплексных чисел.
C
помощью комплексной экспоненты легко
извлекаются корни из комплексных чисел.
Решим уравнение
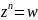 .
Если w=0, то имеется только один нулевой
корень кратности n. Пусть
.
Если w=0, то имеется только один нулевой
корень кратности n. Пусть
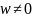 .
Запишем
.
Запишем
 в показательном виде
в показательном виде
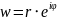 ,
где
,
где
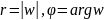 .
Найдем арифметический корень n-ой степени
из r и обозначим его
.
Найдем арифметический корень n-ой степени
из r и обозначим его
 .
Тогда уравнение
имеет n корней, расположенных на окружности
радиуса
.
Тогда уравнение
имеет n корней, расположенных на окружности
радиуса
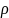 в вершинах правильного n-угольника
в вершинах правильного n-угольника
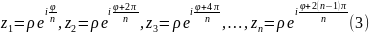
/*/ Действительно,
применяя формулу Муавра, легко проверить,
что все
 -- корни уравнения
-- корни уравнения
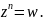 Пусть
Пусть
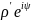 – какой-либо корень уравнения
.
Тогда
– какой-либо корень уравнения
.
Тогда
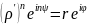 .
Приравнивая модули, получаем равенство
.
Приравнивая модули, получаем равенство
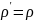 .
Сокращая на
и деля на
,
получим
.
Сокращая на
и деля на
,
получим
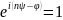 откуда
откуда
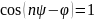 и
и
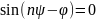 .
Это значит, что
.
Это значит, что
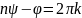 для некоторго целого
для некоторго целого
 .
Поделим
на
.
Поделим
на
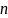 с остатком:
с остатком:
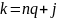 ,
где
,
где
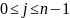 .
Тогда
.
Тогда

и
 .
Следовательно,
.
Следовательно,
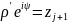 .
.
Корни (3) расположены в вершинах правильного - угольника, вписанного в окружность радиуса , имеющей центр в нулевой точке.
Н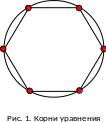 апример,
найдем корни уравнения
апример,
найдем корни уравнения
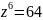 .
Здесь
.
Здесь
 арифметический корень шестой степени
из 64 равен 2, а агрумент
равен нулю. Следовательно, корни имеют
вид
арифметический корень шестой степени
из 64 равен 2, а агрумент
равен нулю. Следовательно, корни имеют
вид

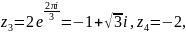
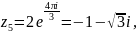
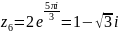
Последовательности и ряды комплексных чисел
Предложение
1. Пусть
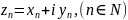 –
последовательность комплексных чисел,
–
последовательность комплексных чисел,
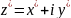 .
Тогда
.
Тогда


Доказательство
вытекает из непрывности отображений
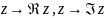 и
и
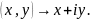 А именно, если
мало, то и
А именно, если
мало, то и
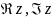 малы, а также если
малы, то
мал (модуль мал). □
малы, а также если
малы, то
мал (модуль мал). □
Предложение 2. Из абсолютной сходимости следует сходимость ряда.
Докажем этот
факт. Обозначим
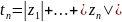 .
Тогда для любого 𝜺
>0 найдется, благодаря критерию Коши,
натуральное N такое, что для любых
.
Тогда для любого 𝜺
>0 найдется, благодаря критерию Коши,
натуральное N такое, что для любых
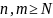 имеет место неравенство
имеет место неравенство
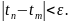 Без ограничения общности можно считать,
что
Без ограничения общности можно считать,
что
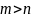 .
Тогда
.
Тогда
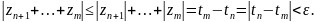
Применяя
снова критерий Коши к ряду
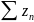 ,
получаем его сходимость. □
,
получаем его сходимость. □
Расширенная комплексная плоскость
Открытую область |z|>R считаем R-окрестностью бесконечно удаленной точки ∞ . Считаем:
z/∞ = 0, ∞ +z=z+∞ =∞ (z∈ ℂ ), c/0 =∞ , ∞ ⋅ c=c⋅ ∞ =∞ (c∈ ℂ *).
Поле комплексных чисел, пополненное элементом ∞, с определенными для него выше правилами, назовем расширенной комплексной плоскостью.
Поместим
комплексную плоскость ℂ
в трехмерное пространство
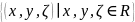 и рассмотрим в этом пространстве сферу
Римана
и рассмотрим в этом пространстве сферу
Римана
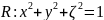 .
Точку N(0,0,1) назовем северным полюсом, а
точку S(0,0,-1) назовем южным полюсом.
Построим стереографическую проекцию
сферы Римана на комплексную плоскость,
т. е. отображение
.
Точку N(0,0,1) назовем северным полюсом, а
точку S(0,0,-1) назовем южным полюсом.
Построим стереографическую проекцию
сферы Римана на комплексную плоскость,
т. е. отображение
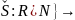 ℂ такое, что для
любой точки P∈ ℜ
, не совпадающей с северным полюсом,
точки N, P и
ℂ такое, что для
любой точки P∈ ℜ
, не совпадающей с северным полюсом,
точки N, P и
 (P)∈
ℂ лежат на одной
прямой. Получаем биективное соответствие
между точками сферы Римана с выброшенным
северным полюсом и точками комплексной
плоскости.
(P)∈
ℂ лежат на одной
прямой. Получаем биективное соответствие
между точками сферы Римана с выброшенным
северным полюсом и точками комплексной
плоскости.
Предложение. Стереографическая проекция задается формулами:

 Если
последовательность точек Pn на
сфере Римана стремится к N, то
Если
последовательность точек Pn на
сфере Римана стремится к N, то
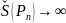 и наоборот, если последовательность
комплексных чисел
и наоборот, если последовательность
комплексных чисел
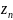 стремится к ∞ , то
стремится к ∞ , то
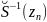 приближается к северному полюсу по
сфере Римана.
приближается к северному полюсу по
сфере Римана.
Дробно-линейная функция
Группа дробно-линейных преобразований сферы Римана
Функция вида
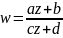 , где a,b,c,d∈
ℂ и ad-bc≠
0, называется дробно-линейной . В
частности, дробно-линейной функцией
будет всякая линейная функция w=az+b
с a≠ 0. Дробно-линейная
функция неопределена в точке -d/c, но
нетрудно вычислить, что предел функции
при
, где a,b,c,d∈
ℂ и ad-bc≠
0, называется дробно-линейной . В
частности, дробно-линейной функцией
будет всякая линейная функция w=az+b
с a≠ 0. Дробно-линейная
функция неопределена в точке -d/c, но
нетрудно вычислить, что предел функции
при
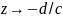 равен ∞. Полагаем по определению
w(-d/c)=∞ и, кроме того, ясно, что w(∞ )=a/c.
Тогда дробно-линейная функция задает
биективное преобразование расширенной
комплексной плоскости.
равен ∞. Полагаем по определению
w(-d/c)=∞ и, кроме того, ясно, что w(∞ )=a/c.
Тогда дробно-линейная функция задает
биективное преобразование расширенной
комплексной плоскости.
Предложение.
Обратная к дробно-линейной функции
также будет дробно-линейной функцией
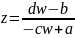 . Композиция дробно-линейных функций
снова будет дробно линейной функцией.
. Композиция дробно-линейных функций
снова будет дробно линейной функцией.
