
- •Поле комплексных чисел
- •Сопряжение комплексных чисел
- •Тригонометрическая форма записи комплексных чисел
- •Комплексная экспонента
- •Извлечение корней из комплексных чисел.
- •Последовательности и ряды комплексных чисел
- •Расширенная комплексная плоскость
- •Дробно-линейная функция
- •Группа дробно-линейных преобразований сферы Римана
- •Инверсия.
- •Аналитичность
- •Гармонические функции
- •Степенные ряды
- •Основные функции комплексной переменной
- •Экспонента
- •Тригонометрические и гиперболические функции
- •Аргумент комплексного числа
- •Многозначные функции
- •Интегрирование функции комплексного переменного
- •Кривые на комплексной плоскости
- •Определение и свойства интеграла
- •Длина кривой
- •Теорема Коши
- •Теорема Коши для односвязной области
- •Распространение на многосвязные области
- •Интегральная формула Коши
- •Ряд Тейлора
- •Теорема единственности и аналитическое продолжение
- •Ряд Лорана
- •Изолированные особые точки
- •1. Особые точки
- •2. Разложение в окрестности особой точки
- •Основная теорема о вычетах
- •Вычисление интегралов с помощью вычетов
- •Литература
Тригонометрическая форма записи комплексных чисел
Изобразим
комплексное число
вектором. Длина этого вектора, т.е.
величина
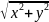 называется модулем комплексного числа
и обозначается
называется модулем комплексного числа
и обозначается
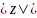 .
Если
.
Если
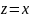 -- действительное число, то приходим к
«школьному» модулю, ибо
-- действительное число, то приходим к
«школьному» модулю, ибо
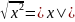 .
Если
.
Если
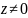 ,
то угол, который образует вектор
с действительной осью называется
аргументом комплексного числа
и обозначается
,
то угол, который образует вектор
с действительной осью называется
аргументом комплексного числа
и обозначается
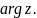 Пусть
Пусть
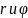 – модуль и аргумент ненулевого
комплексного числа. Тогда
– модуль и аргумент ненулевого
комплексного числа. Тогда
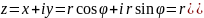 (1)
(1)
Выражение
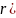 называется
тригонометрической формой записи
комплексного числа.
называется
тригонометрической формой записи
комплексного числа.
Свойства
модуля. Для любых комплексных чисел
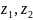 имеют место соотношения:
имеют место соотношения:
а)
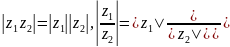 ,
,
б)
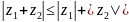 (неравенство треугольника);
(неравенство треугольника);
Докажем первое равенство:
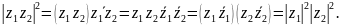
Извлекая
квадратный корень, получим равенство
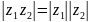 .
Второе равенство следует из первого,
ибо оно эквивалентно следующему
соотношению:
.
Второе равенство следует из первого,
ибо оно эквивалентно следующему
соотношению:
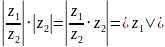 .
.
Докажем
неравенство треугольника. Обозначая
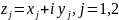 и возводя в квадрат, заменяем это
неравенство на равносильное:
и возводя в квадрат, заменяем это
неравенство на равносильное:
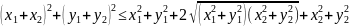
Возводя в квадрат в левой части и сокращая, получаем эквивалентное неравенство
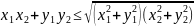
Это неравенство будет следовать из неравенства
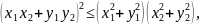
которое, после возведения в квадрат и сокращения, превращается в неравенство

Последнее неравенство несомненно верно. □
Следствие.
Множество комплексных чисел с единичным
модулем (обозначим:
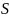 – комплексная единичная окружность)
замкнуто относительно умножения и
обращения.
– комплексная единичная окружность)
замкнуто относительно умножения и
обращения.
Перемножим два комплексных числа в тригонометрической форме записи:

Применяя тригонометрические формулы «косинус суммы» и «синус суммы», приходим к следующему правилу: при перемножении комплексных чисел модули умножаются, а аргументы складываются
(2)
В частности,
перемножая число
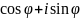 на себя n раз, получаем
формулу Муавра:
на себя n раз, получаем
формулу Муавра:
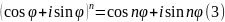
Умножая
произвольное комплексное число-вектор
на комплексное число вида
,
увеличиваем аргумент у комплексного
числа
на величину
 ,
не меняя модуля. Это преобразование
соответствует повороту комплексной
плоскости на угол
,
не меняя модуля. Это преобразование
соответствует повороту комплексной
плоскости на угол
 Умножение на положительное действительное
число
Умножение на положительное действительное
число
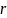 есть гомотетия комплексной плоскости
(растяжение в
раз, если
есть гомотетия комплексной плоскости
(растяжение в
раз, если
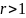 и сжатие в
и сжатие в
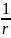 раз, если
раз, если
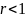 ).
Итак, преобразование
).
Итак, преобразование
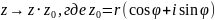
представляет из себя последовательное выполнение двух геометрических преобразований над вектором -- поворота и гомотетии. В этом и заключается геометрический смысл умножения комплексных чисел.
Пример.
Вычислим
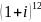 .
Для этого сначала найдем модуль и
аргумент числа
.
Для этого сначала найдем модуль и
аргумент числа
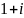 :
:
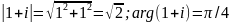
Для того
чтобы найти аргумент изобразим комплексное
число
вектором, очевидно лежащем на биссектрисе
первого квадранта, и ответ
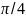 или, по другому,
или, по другому,
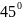 станет понятен. Далее
станет понятен. Далее
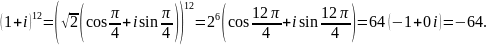
Комплексная экспонента
Правило (2) предыдущего параграфа дает нам право определить экспоненту чисто мнимого числа:
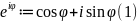
Действительно,
таким образом определенная функция
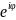 обладает следующими свойствами:
обладает следующими свойствами:
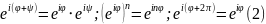
Здесь первое
равенство есть частный случай (2)
предыдущего параграфа, когда
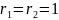 ,
второе равенство есть не что иное как
формула Муавра, а третье равенство
вытекает из периодичности гармоник.
Заметим, что никакой коллизии в обозначения
в связи с известной экспонентой
,
второе равенство есть не что иное как
формула Муавра, а третье равенство
вытекает из периодичности гармоник.
Заметим, что никакой коллизии в обозначения
в связи с известной экспонентой
 действительной переменной не возникает;
равенство аргументов
действительной переменной не возникает;
равенство аргументов
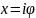 возможно лишь если
возможно лишь если
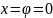 .
Но тогда определение (1) комплексной
экспоненты дает нам значение
.
Но тогда определение (1) комплексной
экспоненты дает нам значение
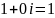 ,
что совпадает с известным равенством
,
что совпадает с известным равенством
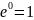 .
.
Определение (1) позволяет записать ненулевое комплексное число в показательной форме
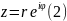
В таком виде легче оперировать с комплексными числами, когда речь идет об умножении, делении и возведении в степень. Например,
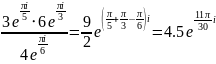
Определим теперь комплексную экспоненту для любого комплексного числа
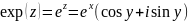
Функция
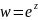 будет уже функцией комплексного
переменного. Для нее справедливы свойства
будет уже функцией комплексного
переменного. Для нее справедливы свойства
Е1. Область определения – все комплексные числа.
Е2.
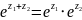 ;
;
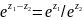
Е3.
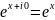 —«школьная
экспонента»
—«школьная
экспонента»
Е4. Комплексная
экспонента периодична с периодом
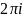
Е5. Область значений – все комплексные числа, кроме нуля
