Практичне заняття 3. Рекомендації щодо виконання розрахунково-графічної роботи з дисципліни

Розрахунково-графічна робота (далі РГР) з дисципліни “Контроль, діагностика та надійність електронної апаратури” складається з 5 основних етапів і дозволяє студентам самостійно провести діагностику обраного електронного пристрою та проаналізувати його режими роботи, особливості функціонування при різних можливих технічних несправностях. Основними етапами РГР є наступні:

1. Вибір об’єкта діагностування. В цьому етапі роботи наводять його призначення, особливості роботи, основні технічні характеристики та режими функціонування. Крім цього на даному етапі необхідно навести принципову електричну схему об’єкта діагностування або його частини, яка є предметом розгляду.

2. Розрахунок інтенсивності відмови об’єкта діагностування за значеннями інтенсивності відмов його окремих елементів. Для розрахунку загальної інтенсивності відмови доцільною є таблиця з довідкових даних виду:

Таблиця 1

Найменування елементу	Величина інтенсивності відмови ×10-6, 1/год
Мікросхема	0,3
Мікропроцесор	0,05
Резистор	0,1
Конденсатор	0,002-0,04

Продовження таблиці 1.

Найменування елементу	Величина інтенсивності відмови, 1/год
Котушка індуктивності	0,00001
Діод	0,3
Трансформатор	0,2
Електронний вимикач	0,3-0,5
Транзистор	0,4
Паяння	0,0001
Роз’єм	3

3. Побудова залежності ймовірності безвідмовної роботи від часу експлуатації для електронних компонентів об’єкта діагностування. В даному етапі треба додатково навести криву загальної ймовірності безвідмовної роботи усього пристрою, який розглядається. На рисунку треба показати координату напрацювання об’єкта діагностики на відмову.

4. Складання таблиці несправностей виду:

Номер несправності	Прояв несправності (ознаки)
1...

5. Складання словника несправностей

Прояв несправності	Технічне обґрунтування можливої несправності

6. Висновки по роботі.

Практичне заняття 4. Показники надійності елементів у випадку довільного розподілу ймовірності безвідмовної роботи

Розглянемо показники надійності для двох класів об’єктів діагностики. Мова йде про об’єкти, які здатні після ремонту виконувати свої функції та об’єкти, які взагалі не підлягають ремонту.

1. Не відновлювальні об’єкти діагностики

Нехай відомий закон розподілу часу роботи об’єкта діагностування до відмови . Введемо наступні позначення:

• заданий час неперервної роботи;

• щільність розподілу ;

• ймовірність безвідмовної роботи в інтервалі часу ;

• середній час безвідмовної роботи;

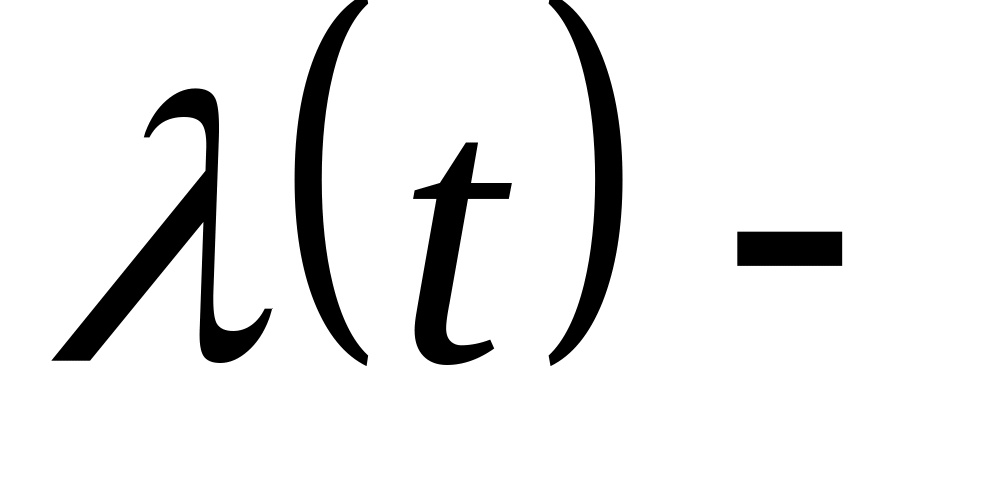• інтенсивність відмови;

• середній час відновлення.

Основні показники надійності.

а) Ймовірність безвідмовної роботи .

б) Ймовірність відмови .

в) Ймовірність безвідмовної роботи в інтервалі роботи від до

. (4.1)

г) Середній час роботи об’єкту до відмови

(4.2)

д) Інтенсивність відмов

.

Якщо функція розподілу задана у вигляді ступінчастої функції, то

(4.3)

Показники надійності у випадку їх статистичного визначення

а) Ймовірність безвідмовної роботи в інтервалі часу функціонування об’єкту від 0 до :

,

де

кількість справних об’єктів у момент часу ;

кількість справних об’єктів у початковий момент часу ;

кількість об’єктів, що відмовили за час .

б) Ймовірність відмови

.

в) Ймовірність відмови в інтервалі часу від до

де

кількість об’єктів, які відмовили саме в інтервалі часу .

г) Щільність розподілу відмов об’єкту

д) Інтенсивність відмов об’єкту у момент часу

Задача 15. Нехай при випробуваннях 35 елементів після кожної години фіксувалася кількість відмов. Результати цих досліджень наведено у таблиці

Момент часу	Кількість відмов
1	0
2	3
3	3
4	5
5	8
6	7
7	6
8	2
9	1
10	0

Знайти функцію розподілу часу роботи елементів до відмови та визначити наступні показники надійності: ймовірність відмови елементів за час спостереження 4 год; ймовірність безвідмовної роботи в інтервалі часу від 2 год до 6 год; середній час роботи елементів до відмови; інтенсивність відмов.

Розв’язок. Функцію розподілу часу можна визначити за наступною формулою:

де кількість елементів, що відмовили за час . У табличному вигляді функція має вигляд:

	1	2	3	4	5	6	7	8	9	10
	0	0,086	0,172	0,314	0,543	0,743	0,914	0,971	1	1

Ймовірність відмови елементів за час спостереження 4 год можна знайти використовуючи дані цієї таблиці

0,314.

Ймовірність безвідмовної роботи в інтервалі часу від 2 год до 6 год можна визначити за допомогою (4.1):

.

Середній час роботи елементів до відмови можемо знайти використовуючи вираз (4.3)

,

де і з умов задачі 1 год. Тобто

1+0,914+0,828+0,786+0,457+0,257+0,086+0,029=4,357 год.

Інтенсивність відмов можна розрахувати за такою формулою:

.

Результати розрахунків представлено у вигляді таблиці:

	1	2	3	4	5	6	7	8	9
	0	3/35	3/32	5/29	8/21	7/16	6/9	2/3	1

Задача 16. Відомо, що закон розподілу часу роботи елемента до відмови є нормальним з середнім значення до відмови 100 год та дисперсією 1000 год². Знайти такі параметри надійності елемента, що розглядається: ймовірність безвідмовної роботи за час, що дорівнює 70 год і 130 год; ймовірність безвідмовної роботи в інтервалі часу від 70 год до 90 год; інтенсивність відмови елемента при 70 год і 130 год роботи.

Розв’язок. Ймовірність безвідмовної роботи за час роботи 70 год і 130 год можна визначити з співвідношення:

де нормована функція нормального розподілу. З довідкових таблиць знаходимо, що

0,829;

0,171.

Ймовірність безвідмовної роботи в інтервалі часу від 70 год до 90 год знаходимо за допомогою виразу (4.1)

Інтенсивність відмови елемента для 70 год і 130 год можна знайти враховуючи значення допоміжної функції:

,

тоді

використовуючи отримане визначимо

2. Відновлювальні об’єкти діагностики

Наведемо лише ті показники надійності, які є характерними для відновлювальних об’єктів діагностики. При цьому параметри, які були наведені для першого класу, наприклад параметр , визначається в даному випадку так само, тобто за тим самим співвідношенням.

Показники надійності.

а) Середній час відновлення

(4.4)

де закон розподілу часу відновлення.

б) Ймовірність безвідмовної роботи

,

де закон розподілу часу між відмовами.

г) коефіцієнт готовності

.

д) коефіцієнт простою

.

є) коефіцієнт оперативної готовності для інтервалу часу тривалістю

(4.5)

Коли і : . На завершення розгляду параметрів надійності дамо визначення цього параметра надійності.

Коефіцієнт оперативної готовності – ймовірність того, що об’єкт виявиться у працездатному стані у довільний момент часу, окрім запланованих періодів, протягом яких використання об’єкта за призначенням не передбачається, і, починаючи з цього моменту він буде функціонувати безвідмовно заданий інтервал часу.

Задача 17. Нехай функція розподілу часу об’єкту до відмови задана у вигляді таблиці:

	1	2	3	4	5	6	7	8	9
	0	0,086	0,172	0,314	0,543	0,743	0,914	0,971	1

Вважається, що час роботи між відмовами об’єкту має такий самий розподіл. Час відновлення є випадковою величиною, і приймає значення 0,1 год з ймовірністю 0,6; 0,2 год з ймовірністю 0,3 і 1,5 год з ймовірністю 0,1. Визначити наступні показники надійності: ймовірність відмови за час спостереження 4 год; ймовірність безвідмовної роботи в інтервалі часу від 2 год до 6 год; середній час роботи до відмови; середній час відновлення; коефіцієнт готовності; коефіцієнт простою; коефіцієнт оперативної готовності за час, що дорівнює 2 год.

Розв’язок. Оскільки за умовою задачі час роботи між відмовами має такий самий розподіл, що і розподіл часу роботи об’єкту до відмови, і до того ж, дані наведеної в умові таблиці повністю співпадають з даними, отриманими в задачі 15 (пункт 1 розв’язку), то відразу знаходимо, що

4,357 год.

Середній час відновлення враховуючи визначення (4.4):

Коефіцієнт готовності можна знайти таким чином

Тоді коефіцієнт простою буде дорівнювати

Коефіцієнт оперативної готовності для 2 год з (4.5) знаходиться як