21.Общая постановка задачи динамического программирования (дп). Особенности задачи дп

ДП – метод оптимизации многошаговых операций. Такие задачи начал рассматривать Беллман в середине 20 века. Объект управления S:S₀→S начальное состояние – конечное состояние. Пусть это управление можно разбить на n шагов, при этом решение будет приниматься на каждом шаге. x_k – решение на каждом шаге, S_k – состояние объекта управления после k шага.

Вводится показатель эффективности управления – целевая функция.

Z = f(S₀,x)→opt (1); x = (x₁, x₂,…,x_n)

Состояние системы после k шага зависит только от состояния системы на предыдущем шаге k-1 и управления. S_k=f_k(S_k-1,x_k)

Прибыль на k шаге зависит от x_k и S_k-1. Z=f_k(S_k-1,x_k)

Прибыль за всю операцию составляет сумма прибыли на каждом шаге

Задача: Определить такое допустимое управление x, приводящее систему из S₀ в S_п, в котором целевая функция (1) принимает свое оптимальное значение. Особенности: Каждая ЗЛП разбивается по n шагов; отсутствует обратная связь, выбор x_k зависит только от x_k-1; Состояние системы зависит S_k зависит от x_k и S_k-1; принцип отсутствие последствия.

22.Принцип оптимальности и уравнения Беллмана

Принцип оптимальности (ПО) – каково бы не было состояние системы в результате какого- либо числа шагов, на очередном поле нужно выбрать x_k чтобы оно в совокупности с x_k+1 приводило к оптимальному значению Z на всех последующих и данном шаге.

Одношаговая задача (последний шаг)

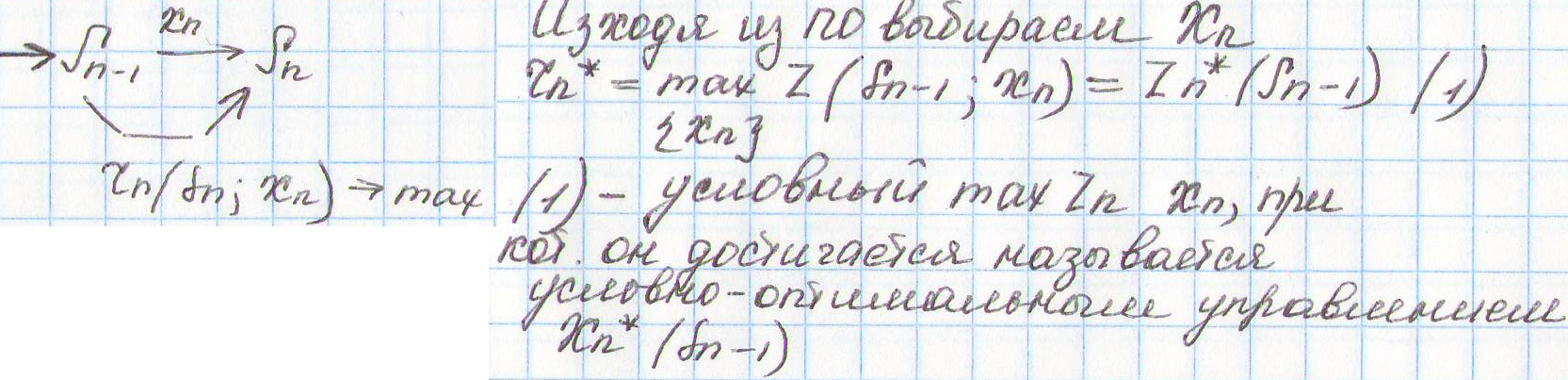
Двух шаговая задача (2 последних шага)

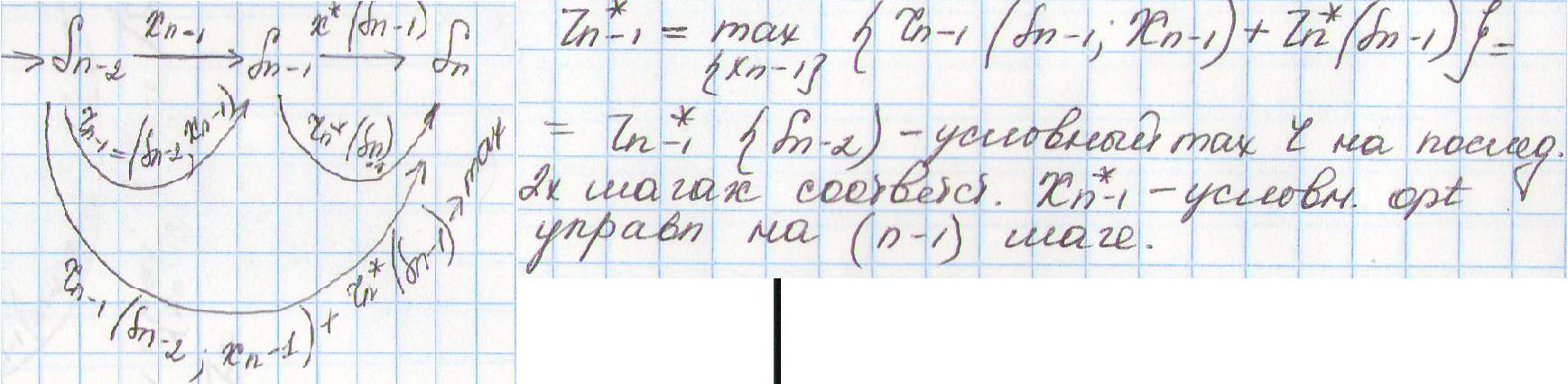
n – шаговая задача

23. Задача о распределении средств между n предприятиями (основные уравнения).

S₀=4д.е., размеры вложений кратны 1д.е.

Х	Z1	Z2	Z3
0	0	0	0
1	6	3	4
2	7	4	6
3	11	7	8
4	13	11	13

X₁ X₂ X₃

S₀->S₁ ->S₂ ->S_{3 ,} S₁ =S0-X1 , S₂ =S1-X2 , S₃ =S2-X3

24. Понятие графа и способы его задания. Степень вершины. Инцидентность. Матрица смежности.

Г раф или неориентированный граф G-это упорядоченная пара G: = (X,U), для которой выполнены следующие условия:

-X это непустое множество вершин или узлов,

-U это множество пар (в случае неориентированного графа — неупорядоченных) вершин, называемых рёбрами.

Графы обычно изображаются в виде геометрических фигур, так что вершины графа изображаются точками, а ребра – линиями, соединяющими те точки, соответствующим вершинам которых ребра инцидентны. Ребро (ab) инциндентно с a, но a с b не инциндентно.

Способы задания графа:

1.явный X={a,b,c,d,e,f}; U={(ab),(ad),(bb),(bc),(bd),(cd),(cd),(ce)}.

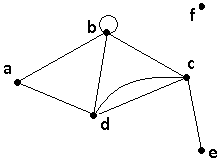2 .графический. Степень вершины- количество рёбер графа G, инцидентных вершине x. Обозначается d(x). d(a)=2.

3.матричный. матрицей смежности графа называется матрица размером n×n, где n-число вершин, а A_ij равен числу ребер инциндентных к обоим вершинам x_i,x_j.

A_n×n={a_ij}, a_ij~x_i,x_j. a_ij-число ребер (x_i,x_j).