
- •Вопросы к экзамену по курсу вм и ппп
- •1. Математическая модель является всего лишь приближенным описанием объекта.
- •3. Применяемые для решения методы как правило являются приближенными.
- •4. При вводе данных при выполнении арифметических операций и при выводе результатов происходит округление.
- •Вида погрешностей:
- •15. Прямые методы решения слау
- •24. Метод релаксации.
- •18. Метод Холецкого для решения слау.
- •20. Компактная схема метода Гаусса для треугольного разложения матрицы системы.
- •21. Метод прогонки.
- •19. Метод Гаусса и lu-разложение.
- •27. Решение проблемы собственных значений для симметричных матриц.
- •28. Решение проблемы собственных значений для матриц общего вида.
- •29. Метод Гивенса
- •30. Метод обратных итераций
20. Компактная схема метода Гаусса для треугольного разложения матрицы системы.

21. Метод прогонки.
Для
трехдиагональных систем. Используется
при решении задач матфизики и аппрокс.
сплайнами
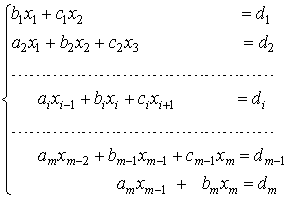

19. Метод Гаусса и lu-разложение.
1. Схема единственного деления (без отбора)
2. С выбором главного элемента по столбцу (схема частичного выбора)
3. –«- по всей матрице (схема полного выбора)


26.
Нормы
векторов и матриц.
Нормой
вектора
![]() называется
число
называется
число
![]() ,
удовлетворяющее трем аксиомам:
1)
,
удовлетворяющее трем аксиомам:
1)
![]() причем
=
0 тогда и только тогда, когда
=
0;
2)
причем
=
0 тогда и только тогда, когда
=
0;
2)
![]() для
любого вектора
и
любого числа
для
любого вектора
и
любого числа
![]() ;
;
3)
![]() для
любых векторов
и
для
любых векторов
и
![]() .
Наиболее
употребительными являются следующие
три нормы:
.
Наиболее
употребительными являются следующие
три нормы:
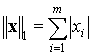 ,
, 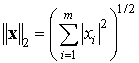 ,
, ![]() .
Абсолютная и относительная
погрешности вектора вводятся с помощью
формул:
.
Абсолютная и относительная
погрешности вектора вводятся с помощью
формул:
![]() и
и 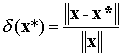 .
.

Нормой
матрицы
![]() называется
величина
называется
величина
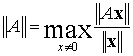 .
Введенная норма обладает свойствами,
аналогичными свойствам нормы вектора:
1)
.
Введенная норма обладает свойствами,
аналогичными свойствам нормы вектора:
1)
![]() причем
причем
![]() =
0 тогда и только тогда, когда A
= 0;
2)
=
0 тогда и только тогда, когда A
= 0;
2)
![]() для
любой матрицы A
и любого числа
;
3)
для
любой матрицы A
и любого числа
;
3)
![]() для
любых матриц A
и B;
4)
для
любых матриц A
и B;
4)
![]() .
Каждой
из векторных норм соответствует своя
подчиненная норма матрицы:
.
Каждой
из векторных норм соответствует своя
подчиненная норма матрицы:
 ,
, ![]() ,
, 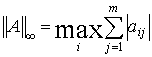 .
В
оценках вместо нормы
.
В
оценках вместо нормы
![]() используется
евклидова норма матрицы
используется
евклидова норма матрицы
 ,
так как
,
так как ![]() .
Абсолютная и относительная
погрешности матрицы вводятся аналогично
погрешностям вектора с помощью
формул:
.
Абсолютная и относительная
погрешности матрицы вводятся аналогично
погрешностям вектора с помощью
формул:
![]() ,
,  .
.
27. Решение проблемы собственных значений для симметричных матриц.
Метод |
Результат |
Примечания |
1. Якоби |
Диагональная форма матрицы |
Теоретически требует бесконечного числа шагов |
2. Гивенса |
Трехдииональльная форма матрицы |
Требует знания корней простого полинома |
3. Хаусхолдера |
Трехдиагональная форма матрицы |
Требует знания корней простого полинома |
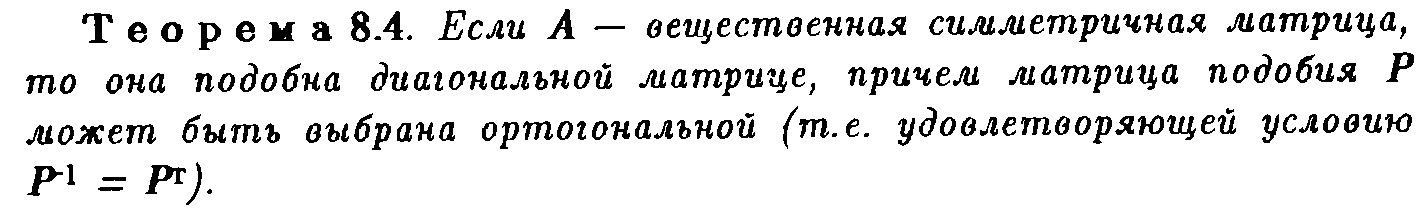



28. Решение проблемы собственных значений для матриц общего вида.
Метод |
Результат |
Примечания |
1.Классика |
Собственные значения |
Требует нахождения корней полинома общего вида |
2.Обратных итераций |
Собственные значения и собственные векторы |
Оптимален, когда есть прибл. значение собств. числа |
3.Степенной (в т.ч. со сдвигом) |
Макс. по модулю собственное число |
|
4. QR |
Квазидиагональная форма матрицы |
Лучший метод, обладающий наибольшей общностью |
5. LR |
-“- |
Бывает неустойчив |
Вещественное число λ и вектор z называются собственной парой матрицы A, если они удовлетворяют следующему условию: Az = λz. При этом для вещественной матрицы A может быть поставлена задача поиска только собственных чисел, или как собственных чисел, так и векторов.

1. Все п собственных значений симметричной матрицы размерности пХп, состоящей из действительных чисел, действительные. Это полезно помнить, так как матрицы, встречающиеся в инженерных расчетах, часто бывают симметричными.
2. Если собственные значения матрицы различны, то ее собственные векторы ортогональны. Совокупность п линейно независимых собственных векторов образует базис рассматриваемого пространства. Следовательно, для совокупности линейно независимых собственных векторов
Xi, где i == 1,. . ., n,
любой произвольный вектор в том же пространстве можно выразить через собственные векторы.
