
- •Вопросы к экзамену по курсу вм и ппп
- •1. Математическая модель является всего лишь приближенным описанием объекта.
- •3. Применяемые для решения методы как правило являются приближенными.
- •4. При вводе данных при выполнении арифметических операций и при выводе результатов происходит округление.
- •Вида погрешностей:
- •15. Прямые методы решения слау
- •24. Метод релаксации.
- •18. Метод Холецкого для решения слау.
- •20. Компактная схема метода Гаусса для треугольного разложения матрицы системы.
- •21. Метод прогонки.
- •19. Метод Гаусса и lu-разложение.
- •27. Решение проблемы собственных значений для симметричных матриц.
- •28. Решение проблемы собственных значений для матриц общего вида.
- •29. Метод Гивенса
- •30. Метод обратных итераций
15. Прямые методы решения слау
Прямые (или точные) методы, позволяют найти решение за определённое количество шагов. Итерационные методы, основаны на использовании повторяющегося процесса и позволяют получить решение в результате последовательных приближений.
Формальное решение строится по формулам Крамера
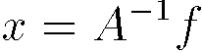
Метод Гаусса (приведение матрицы к треугольному виду и послед. Нахождения корней) a. Прямой метод b.обратный метод(Жордана - Гаусса)
LU разложение это Ax=LUx=f, где U-треугольная матрица приведенная по методу Гаусса. Ux=y, где y это столбец свободных коэфицентов полученный из f методом Гаусса (
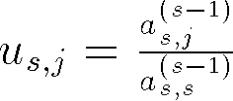 ;
; )
)Метод квадратного корня (метод Холецкого)
Метод с ленточной матрицей (метод прогонки)
Сокращённый метод Гаусса
Метод Холецкого для симметр. Матриц
16. Итерационные методы решения СЛАУ.
Метод Гаусса-Зейделя
Метод релаксации (обобщение м. Зейделя)
Метод уточнения решения полученного прямым методом
Метод плоских вращения (Якоби)
Циклический метод Якоби с барьерами (более эффективен в случаях большой размерности)
Метод Гивенса
Метод обратных итераций
Другие двухслойные методы (м. минимальных невязок и поправок, м. скорейшего спуска, м. сопряженных градиентов…)
24. Метод релаксации.
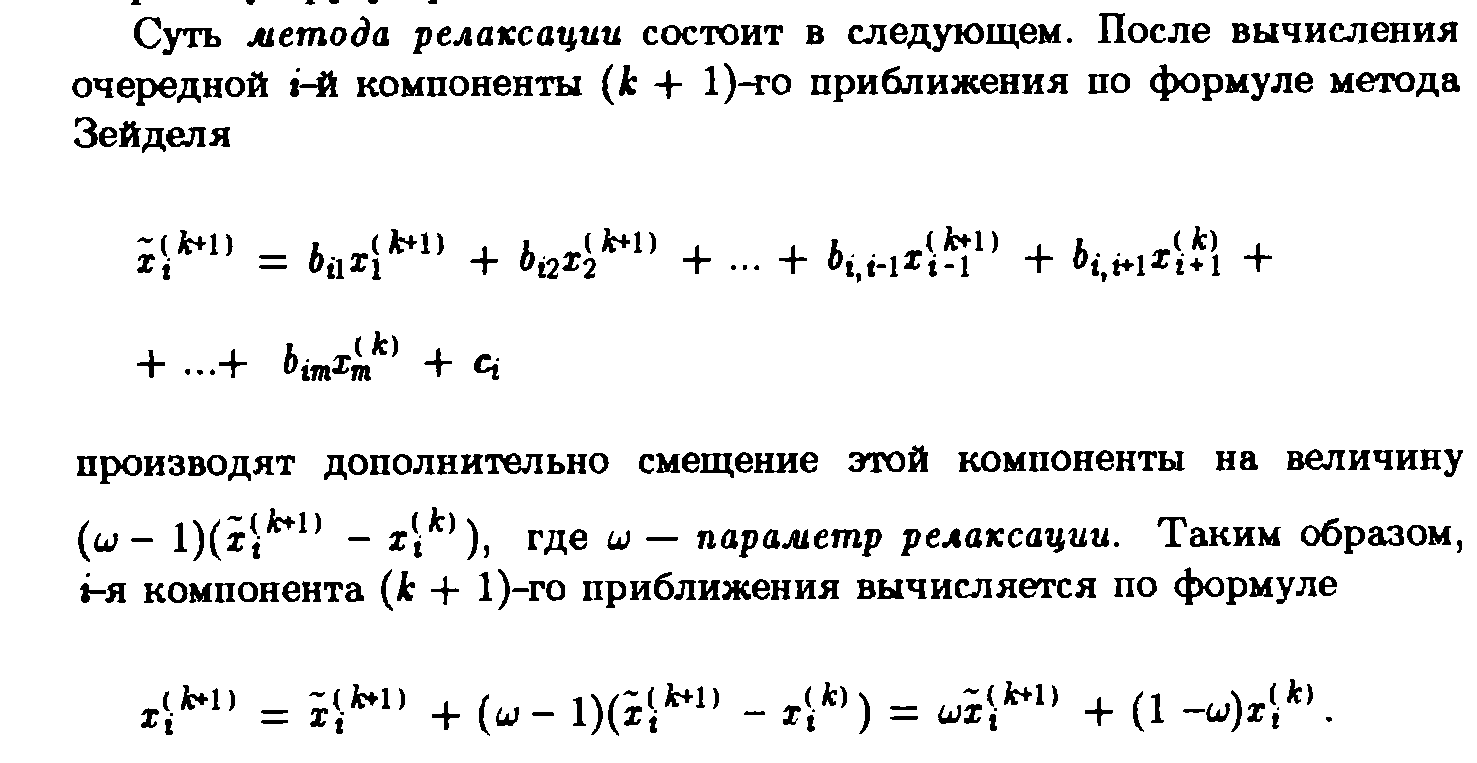
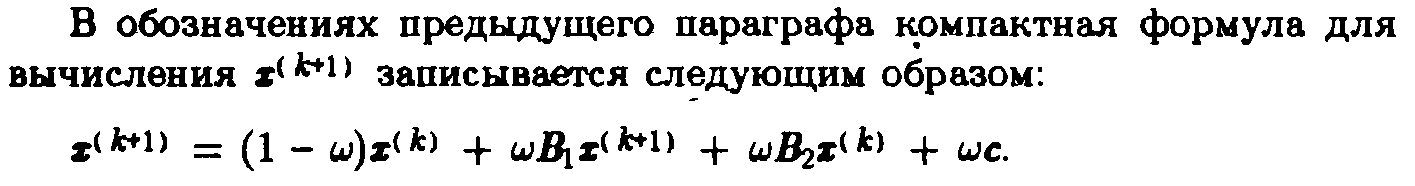
17. Каноническая форма итерационных методов.
Канонический вид одношаговых итерационных методов для решения системы линейных алгебраических уравнений Ax = f
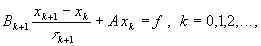
где Вк+1 - квадратная матрица n n , k+1 > 0 - итерационный параметр. В дальнейшем будем использовать следующие согласованные нормы в конечномерном пространстве размерности n:
Итерационный
метод сходится, если
![]() .
.
Опр. Величина zk = xk - x называется погрешностью решения.
Опр. Если Bk+1 = B и k+1 = то метод называется стационарным
Метод Зейделя

Метод релаксации
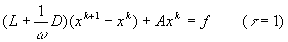
Метод простой итерации
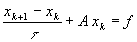
Метод Якоби
18. Метод Холецкого для решения слау.
Если
матрица системы является симметричной
и положительно определенной, то для
решения системы применяют метод
Холецкого (метод квадратных корней). В
основе метода лежит алгоритм специального
LU-разложения
матрицы A,
в результате чего она приводится к виду
A=![]() .
Если разложение получено, то как и в
методе LU-разложения,
решение системы сводится к последовательному
решению двух систем с треугольными
матрицами:
.
Если разложение получено, то как и в
методе LU-разложения,
решение системы сводится к последовательному
решению двух систем с треугольными
матрицами:
![]() и
и
![]() .
Для нахождения коэффициентов матрицы
L неизвестные
коэффициенты матрицы
приравнивают
соответствующим элементам матрицы A.
Затем последовательно находят требуемые
коэффициенты по формулам:
.
Для нахождения коэффициентов матрицы
L неизвестные
коэффициенты матрицы
приравнивают
соответствующим элементам матрицы A.
Затем последовательно находят требуемые
коэффициенты по формулам:
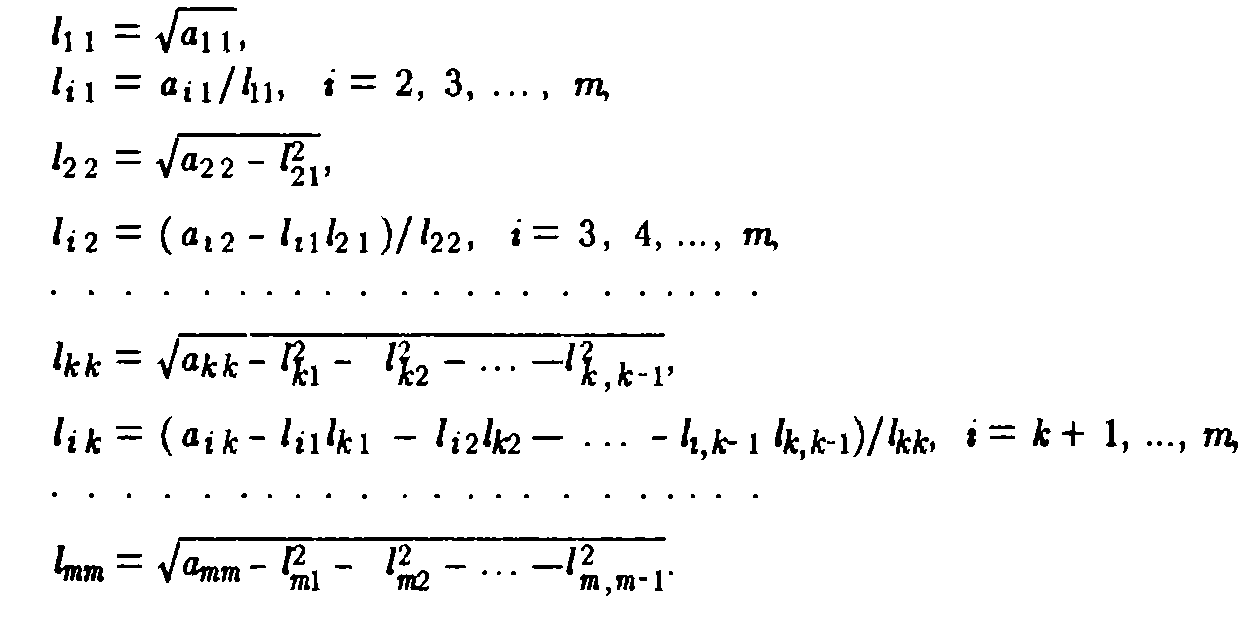
Д остоинства:
1) вдвое меньше выч. затрат 2) симм. матрицы
А экономит память 3) гарант. устойчивость
остоинства:
1) вдвое меньше выч. затрат 2) симм. матрицы
А экономит память 3) гарант. устойчивость
