14) Емкостный элемент в электрической цепи. Энергетические характеристики.

Под емкостным элементом электрической цепи по­нимают идеализированный элемент, в котором происходит только запасание электрической энергии, зависящей от напряжения, а потери и запасание магнитной энергии отсутствуют. Близок к этому идеальному устройству электрический кон­денсатор с хорошим диэлектриком при относительно невысоких частотах.

В случае приложения к конденсатору напряжения на его обкладках появляются заряды, равные по значению и противо­положные по знаку, и в диэлектрике между обкладками образуется связанное с этими зарядами электрическое поле. Так как напряженность электрического поля пропорциональна напряжению между обкладками, заряд на обкладках конденсато­ра будет пропорционален на­пряжению:

q=Cu. (1.18)

Коэффициент пропорцио­нальности между зарядом и напряжением, равный отноше­нию C=q/u, представляет со­бой емкость. В СИ она выражается в фарадах (Ф). Значение емкости является основным параметром емкостного элемента, условное графическое обозначение которого представлено на рис. 1.7, а.

Для установления связи между током и напряжением в емкостном элементе достаточно продифференцировать выра­жение (1.18). В результате получим зависимость тока в емкости от напряжения на ней:

(1.19)

Ток в емкостном элементе определяется скоростью измене­ния напряжения. В случае приложения постоянного напряжения ток в емкости равен нулю и элемент должен представляться разрывом.

Если задан ток, то, проинтегрировав обе части выражения (1.19) в пределах от — до t, найдем напряжение на емкости:

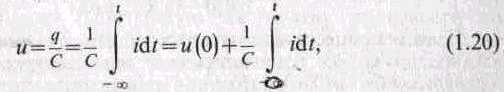
где и (0) =q(0)/С—начальное напряжение на емкости (при t=0), учитывающее все процессы до момента времени t=0.

Напряжение емкостного элемента определяется значениями тока при t>0 и напряжения при t=0; закон изменения тока до момента времени t=0 не играет роли.

Рассмотренный для индуктивного элемента пример можно применить и для емкостного элемента, если заменить на рис. 1.6, а, б ток напряжением, а напряжение—током. В случае приложения напряжения трапецеидальной формы ток емкости (зарядный ток) будет иметь вид прямоугольных импульсов, положительных при нарастании напряжения (зарядке емкости) и отрицательных при спадании напряжения (разрядке емкости).

Выражения (1.19) и (1.20) позволяют установить условие непрерывности заряда в емкостном элементе: при протекании в емкости тока конечной амплитуды заряд должен быть непре­рывной функцией и не может изменяться скачком; выразив, согласно (1.20), заряд в момент времени t=0+ через его значение в момент времени t=0—, получим

Это условие можно записать через напряжение, если обозначить через C_(-), С₍₊₎ значения емкостей до и после коммутации:

С_(-)u(0-)=C₍₊₎u(0+). (1.22)

Если в процессе коммутации значение емкости не изменяется, (С_(-)=С₍₊₎), то напряжение на емкости также будет непрерывным: и(0—)=и(0+). Приведенные условия непрерывности заряда и напряжения используются далее при определе­нии произвольных постоянных интегрирования.

Для момента времени t=0 емкостный элемент в силу непрерывности его напряжения можно заменить источником напряжения с напряжением u(0) или коротким замыканием, если u(0)=0.

Мощность емкостного элемента

(1.23)

Мощность положительна в интервалах нарастания энергии, когда энергия поступает от источника в элемент, и отрицатель­на в интервалах убывания энергии, когда запасенная энергия отдается обратно источнику.

Интегрирование выражения (1.23) в пределах от — до t позволяет найти в предположении u(—)==0 энергию, запасен­ную в емкости:

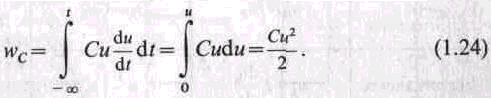
Энергия в емкости определяется мгновенным значени­ем напряжения; она пропорциональна квадрату напряже­ния и поэтому не может принимать отрицательных значе­ний.