
- •Непрерывные функции Определения
- •Типы разрывов
- •Свойства непрерывных функций. Непрерывность сложной функции
- •Теоремы о непрерывных функциях
- •Равномерная непрерывность. Теорема Кантора
- •Монотонные функции
- •Обратная функция. Теорема о существовании обратной функции у монотонной функции
- •Непрерывность элементарных функций
- •Замечательные пределы
- •Типы неопределенных выражений
Замечательные пределы
Рассмотрим еще некоторые пределы, которые полезно знать.
Вспомним замечательный предел
![]()
Сделаем
в нем "замену переменных"
![]() .
Тогда при
.
Тогда при
![]()
![]() и
мы получим
и
мы получим
![]()
Вспомним, что loga – непрерывная функция. Логарифмируя предыдущее равенство, получим:
![]()
Итак,
![]()
В частности,
![]()
В предыдущем соотношении сделаем снова замену переменных
 .
Тогда при
.
Тогда при
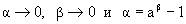 получаем
получаем
![]()
Переворачивая это соотношение, получим
![]() ,
,
В частности,
![]() .
.
Докажем, что
![]()
положим
![]() .
.
Тогда
при x0
y0.
Далее
![]() ,
и логарифмируя это равенство, получим
,
и логарифмируя это равенство, получим
ln(1+x)=ln(1+y)
Далее имеем
![]()
так как оба написанных предела равны 1.
Докажем, что при a>1 и при >0
![]()
а)
Докажем сначала, что при a>1
![]() .
Действительно, обозначим a=1+,
>0.
Пользуясь формулами
бинома Ньютона,
получим
.
Действительно, обозначим a=1+,
>0.
Пользуясь формулами
бинома Ньютона,
получим
![]() .
.
Поэтому![]() , ,
, ,
т.е.
![]() .
.![]()
б) Возьмем произвольное x+ и обозначим n=[x], т.е. целая часть от x. Тогда n x n+1 и получаем
![]() ,
,
так
что
![]() .
Поэтому
.
Поэтому
![]() .
.
в) Наконец, при произвольном >0 имеем

Докажем, что при >0 и a>1
![]()
Действительно, делая замену переменных loga(x)=y, x=ay, получим, что при x, y
![]()
Докажем, что при >0 и a>1
![]()
Действительно,
делая замену переменных
![]()
![]()
Типы неопределенных выражений
При решении различных практических задач большую роль играют так называемые неопределенные выражения или, коротко, неопределенности. Рассмотрим основные их типы.
Пусть имеются две функции u(x) и v(x).
Пусть
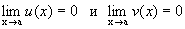 .
Тогда предел вида
.
Тогда предел вида
 называется
неопределенностью типа
называется
неопределенностью типа
 .
Процесс вычисления этого предела
называется "раскрытием неопределенности".
Разумеется, что формула
.
Процесс вычисления этого предела
называется "раскрытием неопределенности".
Разумеется, что формула
 здесь
неприменима. так как
здесь
неприменима. так как
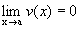
Пусть
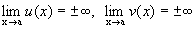 .
Тогда предел вида
называется
неопределенностью типа
.
Тогда предел вида
называется
неопределенностью типа .
.Пусть
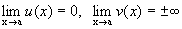 .
Тогда предел вида
.
Тогда предел вида
 называется
неопределенностью типа
называется
неопределенностью типа
 .
Разумеется, и здесь нельзя пользоваться
формулой
.
Разумеется, и здесь нельзя пользоваться
формулой
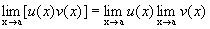
Степенные неопределенности.
Рассмотрим
теперь предел вида
![]() .
.
Так
как![]() ,
то, пользуясь непрерывностью функции
ex,
можно записать
,
то, пользуясь непрерывностью функции
ex,
можно записать
![]() .
.
Это можно сформулировать в виде следующего правила: для вычисления предела выражения вида u(x)v(x) надо это выражение сначала прологарифмировать.
Какие же неопределенности могут иметь здесь место? Так как приходится вычислять lim[u(x)v(x)], а здесь возможна только неопределенность типа , то возможны следующие варианты.
 .
Последнее означает, что
.
Последнее означает, что
 и
поэтому говорят, что мы имеем дело с
неопределенностью типа
и
поэтому говорят, что мы имеем дело с
неопределенностью типа
 .
.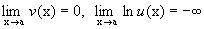 .
Последнее означает, что
.
Последнее означает, что
 и
поэтому говорят, что мы имеем дело с
неопределенностью типа 00.
и
поэтому говорят, что мы имеем дело с
неопределенностью типа 00. .
Последнее означает, что
.
Последнее означает, что и поэтому говорят, что мы имеем дело с
неопределенностью типа 1.
и поэтому говорят, что мы имеем дело с
неопределенностью типа 1.
