
- •Непрерывные функции Определения
- •Типы разрывов
- •Свойства непрерывных функций. Непрерывность сложной функции
- •Теоремы о непрерывных функциях
- •Равномерная непрерывность. Теорема Кантора
- •Монотонные функции
- •Обратная функция. Теорема о существовании обратной функции у монотонной функции
- •Непрерывность элементарных функций
- •Замечательные пределы
- •Типы неопределенных выражений
Равномерная непрерывность. Теорема Кантора
Разберем теперь важное и сложное понятие равномерной непрерывности.
Пусть имеется функция f(x), которая непрерывна на некотором множестве Х. Вспомним, что это означает: это означает, что f(x) непрерывна в каждой точке этого множества и записывается так:
![]()
Обратим внимание на величину стоящую после квантора . От чего она зависит?
Общее
правило гласит, что величина,стоящая
после квантора
зависит
от всех величин, которые стоят после
квантора
,
которые расположены впереди
квантора
.
В данном случае перед
стоят
два квантора
![]() .
Поэтому зависит
от
и, и это самое главное, от х0,
т.е. ,x0).
.
Поэтому зависит
от
и, и это самое главное, от х0,
т.е. ,x0).
Так вот, эта зависимость от х0 очень сильно мешает при доказательстве многих теорем. Хотелось бы, чтобы зависело только от и не зависело от х0, т.е. было бы одинаково пригодно для всех х0 Х. Это желание избавиться от зависимости от х0 и приводит к понятию равномерной непрерывности.
Определение. Функция f(x) называется равномерно непрерывной на множестве Х, если
![]() .
.
Обратите
внимание на то, куда преместился квантор
.
Теперь он стоит после
квантора
![]() и
поэтому зависит
теперь только
от
и не
зависит
от х0.
Это местоположение квантора
и
есть главное в понятии равномерной
непрерывности f(x) на множестве Х.
и
поэтому зависит
теперь только
от
и не
зависит
от х0.
Это местоположение квантора
и
есть главное в понятии равномерной
непрерывности f(x) на множестве Х.
А теперь докажем достаточно сложную теорему о равномерной непрерывности f(x).
Теорема Кантора. Пусть функция f(x) определена и непрерывна на замкнутом отрезке [a,b]. Тогда она равномерно непрерывна на этом отрезке.
Доказательство.
Доказательство этой теоремы проведем методом от противного.
Надо доказать:
![]()
Противоположное утверждение:
![]()
Построение последовательностей.
Возьмем любую последовательность n, которая монотонно убывает до нуля, т.е.
1>2>3>…n0, n
Тогда для каждого n
![]()
Перебирая
все n
мы
получим две
последовательности {xn}
и
![]() .
.
Выделение сходящихся подпоследовательностей.
Рассмотрим
последовательность {xn}.
Она ограничена, т.к.
![]() a
xn
b.
По лемме Больцано-Вейерштрасса,
из нее можно выделить сходящуюся
подпоследовательность
a
xn
b.
По лемме Больцано-Вейерштрасса,
из нее можно выделить сходящуюся
подпоследовательность
![]() ,
т.е.
,
т.е.
![]() .
Заметим, что c[a,b]
в силу замкнутости [a,b]. А что можно
сказать о подпоследовательности
.
Заметим, что c[a,b]
в силу замкнутости [a,b]. А что можно
сказать о подпоследовательности
![]() ?
Т.к.
?
Т.к.
![]() ,
то
,
то
![]() .
.
Но
так как
![]() а
а
![]() то
по
теореме “о двух милиционерах”
отсюда следует, что также
то
по
теореме “о двух милиционерах”
отсюда следует, что также
![]() ,
т.е. подпоследовательность
сходится
к тому же пределу c, что и
.
,
т.е. подпоследовательность
сходится
к тому же пределу c, что и
.
Сведение к противоречию.
Рассмотрим теперь последний квантор
![]()
Переходя к пределу k и учитывая непрерывность функции y=|x|, получим:
![]()
![]()
В
силу непрерывности f(x)
![]() ,
так что получаем, что
,
так что получаем, что
|f(c)-f(c)|
т.е.
получаем, что 0.
Это противоречит квантору
![]() ,
где строго
больше 0.
,
где строго
больше 0.
Монотонные функции
Докажем теперь две теоремы, касающиеся непрерывности монотонных функций.
Теорема 1.. Пусть f(x) определена и монотонна на замкнутом отрезке [a,b]. Тогда она может иметь на этом отрезке только разрывы I рода (скачки).
Доказательство.
Пусть, для определенности, f(x) монотонно возрастает.
 Возьмем
какую-то точку x0[a,b].
Пусть мы приближаемся к точке х0
слева
(см. рис.). Тогда при этом значения функции
f(x) будут монотонно возрастать.
Но они будут ограничены сверху, например,
величиной f(x0).
Поэтому, по теореме о пределе
монотонно-возрастающей функции будет
существовать конечный
Возьмем
какую-то точку x0[a,b].
Пусть мы приближаемся к точке х0
слева
(см. рис.). Тогда при этом значения функции
f(x) будут монотонно возрастать.
Но они будут ограничены сверху, например,
величиной f(x0).
Поэтому, по теореме о пределе
монотонно-возрастающей функции будет
существовать конечный
![]() .
.
При
движении к х0
справа
значения f(x) будут монотонно убывать,
но будут ограничены снизу
величиной f(x0).
Поэтому снова существует конечный![]() .
.
Если f(x0+0)= f(x0-0), то f(x) будет непрерывна в точке х0, если же f(x0+0)<f(x0-0), то у f(x) в точке х0 будет разрыв I рода.
Определение. Говорят, что значения функции f(x), определенной на <a,b>, заполняют некоторый отрезок <c,d> сплошь, если
![]() .
.
Теорема 2. Для того, чтобы монотонная функция f(x) была непрерывной на [a,b], необходимо и достаточно, чтобы ее значения заполняли отрезок [f(a), f(b)] сплошь.
Доказательство.
Пусть, для определенности, f(x) монотонно возрастает.
Пусть f(x) непрерывна на [a,b]. Тогда
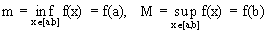 .
Согласно второй теореме Больцано-Коши,
.
Согласно второй теореме Больцано-Коши,
 .
Поэтому отрезок [f(a),f(b)] заполнен сплошь.
.
Поэтому отрезок [f(a),f(b)] заполнен сплошь.Пусть f(x) не является непрерывной на [a,b]. Тогда она на [a,b] может иметь только разрывы I рода. Пусть х0 – координата такого разрыва. Возможные поведения графика f(x) изображены на рисунках.

Из них видно, что в этом случае отрезок [f(a), f(b)] заполнен не сплошь.
