2.5 Определение вариаций параметров по показателям качества.
По графику переходного процесса САР определяем:
m - запас устойчивости по модулю;
Δ
-
запас устойчивости по фазе Δ
;
m=0,45
Δ
=
3 Синтез и анализ прогнозирующей сар Смита.
3.1 Синтезирование структуры и параметров прогнозирующей сар
Если объект управления с запаздыванием таков, что невозможно измерить никакой величины содержащей запаздывание, то используется регулятор Смита. Идея этого регулятора основана на следующем: если ни одна вспомогательная величина не содержит запаздывания, недоступна для измерения, то ее следует создать искусственно. С этой целью необходимо достаточно точно знать математическую модель объекта и той которая содержит запаздывание, а также нужно знать точно величину запаздывания. Значение реакции системы без запаздывания позволяет регулятору предвидеть будущее поведение системы.
Рассмотрим подробно САР Смита.
y
*
+
y
y
- +
прогнозатор
Смита
Рисунок №25
φτ, φ0 – передаточная функция запаздывающей части объекта и объекта без запаздывания.
ƒ – оператор регулирующего блока (например ПИ регулятор)
W– приведенное по входу возмещение.
–
модель объекта управления.
Если модель объекта адекватна самому объекту, то
=
,
φ0=φ0 .
Вначале проанализируем работу регулятора Смита, на основе блок схемы можно записать систему уравнений выхода.
Пусть выполняются условия адекватности, тогда исключая промежуточные переменные получим следующие уравнения:
y(s)
=
∙ y*(s)
+ 
w(s)
если
ƒ(j
)
φ(j
)
1,
то
y(s)
(s)
Таким образом, переходные процессы, вызванные скачкообразным изменением задающего воздействия, заканчиваются за время равное времени запаздывания τ, а переходные процессы вызванные скачкообразным изменением возмещения если объект содержит только запаздывание, то есть φ0=k0 , φ2=e-23 заканчивается в течении 2τ . Следовательно, регулятор Смита оптимален в смысле минимума времени регулирования, так как дальнейшее уменьшение времени не возможно. Убедиться в этом можно с помощью следующего рассуждения.
На прохождение через объект с одним запаздыванием τ возмущающее воздействие затратит время τ.
Таким образом, только через время τ регулятор узнает о действии возмущения. Если регулятор вырабатывает оптимальный управляющий сигнал, то он после прохождения через объект, то есть опять через время τ ликвидирует появившуюся ошибку управления вызванную возмущением, следовательно в сумме окончание переходного процесса может наступить через минимальное время равное 2τ.
3.2 Построение переходного процесса сар Смита
Для того чтобы построить переходный процесс построим дискретные модели.
1)
y(i)=
*
y( i-1) + 
(U
( i-
)
+ W (i-
)
)
Где i=0,1…3500
В качестве регулирующего блока рассмотрим ПИ – регулятор:
2)
U(i) = 
(i)
+ 
(i);
(i)
= 
;
;
;
3)
(i)
= ε(i) - 
;
ε(i) = 
;
4)
;
5)
Моделируем САР при условии, что наша модель адекватна реальному объекту.
Рассчитываем все вышеперечисленные параметры. По полученным данным строим переходный процесс САР Смита при условии i=0,1…3500.
График переходного процесса САР Смита представлен на рисунке.
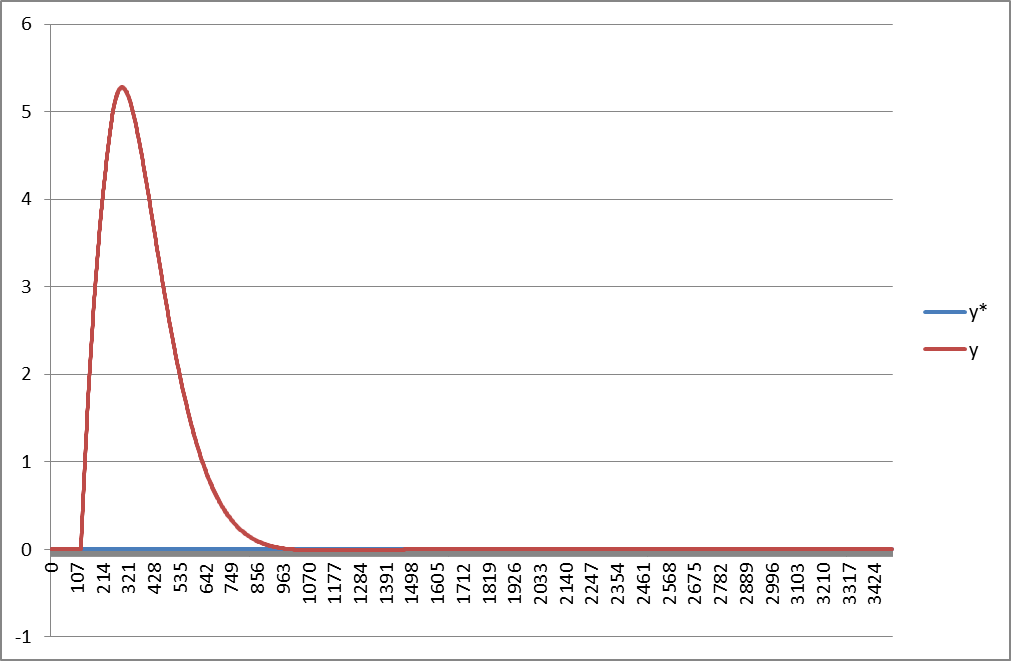
Рисунок №26 - График переходного процесса САР Смита