20) Схема Горнера(вывод формул)

Если

то при делении f(x) на g(x) частное q(x) имеет вид

где

Остаток r находится по формуле

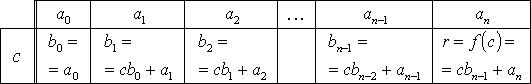
21) Рациональные корни многочленов с целыми коэффициентами.

Теорема о рациональных корнях многочлена

Если многочлен

с целыми коэффициентами имеет рациональный корень x0=p/q, то число p является делителем числа a0 (свободного члена), а число q является делителем числа An (старшего коэффициента).

Доказательство.

Замечание. Эта теорема фактически позволяет находить корни многочленов высших степеней в том случае, когда коэффициенты этих многочленов − целые числа, а корень − рациональное число.

Теорему можно переформулировать так: если нам известно, что коэффициенты многочлена − целые числа, а корни его − рациональны, то эти рациональные корни могут быть только вида x0=p/q где p является делителем числа a0 (свободного члена), а число q является делителем числа An (старшего коэффициента).

Пусть все коэффициенты многочлена являются целыми числами, и пусть целое число a является корнем этого многочлена.

Так как в этом случае то отсюда следует, что коэффициент A0 делится на a.

22) Обобщенная теорема Виета для многочлена n-й степени.

Если и - корни многочлена (каждый кратный корень взят здесь столько раз, какова его кратность), то:

В частности, при при