10. Додатньо та від’ємно визначена матриця Гессе. Використання цих ознак матриці для дослідження функції на екстремум.

будується матриця Гессе, що має блочну структуру розмірністю : де О — матриця розмірністю , що складається з нульових елементів,

Р — матриця розмірністю , елементи якої визначаються так:

,— транспонована матриця до Р розмірністю ,

Q — матриця розмірністю виду:

, де .

Розглянемо ознаки виду екстремуму розв’язку системи. Нехай стаціонарна точка має координати і .

1. Точка є точкою максимуму, якщо, починаючи з головного мінору порядку (m + 1), наступні (n – m) головних мінорів матриці Н утворюють знакозмінний числовий ряд, знак першого члена якого визначається множником .

2. Точка є точкою мінімуму, якщо, починаючи з головного мінору порядку (m + 1), знак наступних (n – m) головних мінорів матриці Н визначається множником .

11. Загальний запис лінійної оптимізаційної моделі. Цільова функція та система обмежень.

Загальна лінійна економіко-математична модель економічних процесів та явищ — так звана загальна задача лінійного програмування подається у вигляді:

(1.1)

за умов:

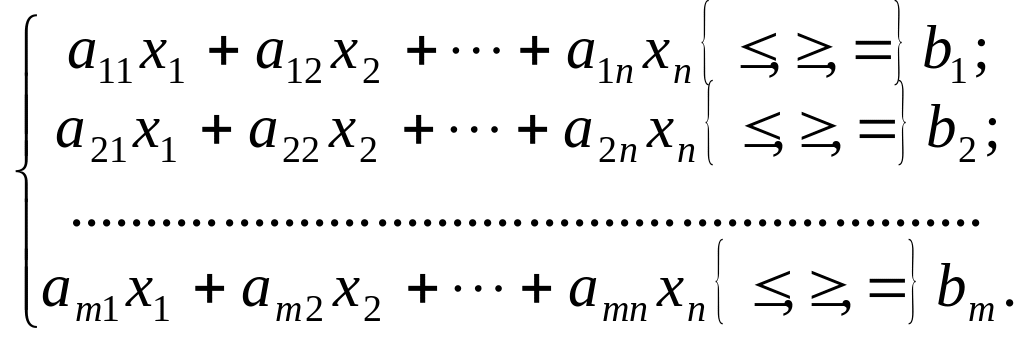(1.2)

(1.3)

Отже, потрібно знайти значення змінних x₁, x₂, …, x_n, які задовольняють умови (1.2) і (1.3), і цільова функція (1.1) набуває екстремального (максимального чи мінімального) значення.

Для довільної задачі математичного програмування були введені поняття допустимого та оптимального планів.

Задачу (1.1)—(1.3) можна легко звести до канонічної форми, тобто до такого вигляду, коли в системі обмежень (1.2) всі b_i (i = 1, 2, …, m) невід’ємні, а всі обмеження є рівностями.

Якщо якесь b_i від’ємне, то, помноживши i-те обмеження на (– 1), дістанемо у правій частині відповідної рівності додатне значення. Коли i-те обмеження має вигляд нерівності а_i1х₁ + а_i2х₂ + … + а_inx_n ≤ b_i, то останню завжди можна звести до рівності, увівши додаткову змінну x_{n + 1}: a_i1x₁ + a_i2x₂ + … + + a_in x_n + x_{n + 1} = b_i.

Аналогічно обмеження виду а_k1x₁ + a_k2x₂ + … + a_knx_n ≥ b_k зводять до рівності, віднімаючи від лівої частини додаткову змінну х_n + 2, тобто: a_k1x₁ + a_k2x₂ + … + a_knx_n – x_{n + 2} = b_k (х_n+1 ≥ 0, х_n+2 ≥ 0).

12. Описати алгоритм розв’язання цілочислових задач лінійного програмування за методом Гоморі.

Розглянемо алгоритм, запропонований Гоморі, для розв’язування повністю цілочислової задачі лінійного програмування, що ґрунтується на використанні симплексного методу і передбачає застосування досить простого способу побудови правильного відтинання.

Нехай маємо задачу цілочислового програмування:

(6.5)

за умов: , (6.6)

, (6.7)

— цілі числа . (6.8)

Допустимо, що параметри — цілі числа.

Не враховуючи умови цілочисловості, знаходимо розв’язок задачі (6.5)—(6.7) симплексним методом. Нехай розв’язок існує і міститься в симплексній таблиці.

Розглянемо довільний оптимальний план задачі (6.5) —(6.7). Виразимо в цьому плані базисну змінну через вільні змінні:

. (6.9)

Виразимо коефіцієнти при змінних даного рівняння у вигляді суми їх цілої та дробової частин. Введемо позначення: — ціла частина числа , — дробова частина числа ². Отримаємо:

, (6.10)

або

. (6.11)

Отже, рівняння (6.11) виконується для будь-якого допустимого плану задачі (6.5)—(6.7). Допустимо тепер, що розглянутий план є цілочисловим оптимальним планом задачі. Тоді ліва частина рівняння (6.11) складається лише з цілих чисел і є цілочисловим виразом. Отже, права його частина також є цілим числом і справджується рівність:

, (6.12)

де N — деяке ціле число.

Величина N не може бути від’ємною. Якщо б , то з рівняння (6.12) приходимо до нерівності:

.