2. Уравнения движения газа.
Для их получения применим второй закон Ньютона к элементарной жидкой частице, имеющей в некоторый момент форму куба с гранями (рис. 3.1).
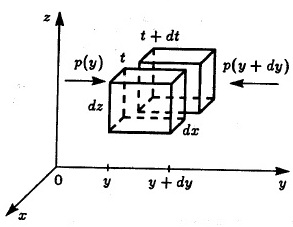
Рис. 3.1
Жидкая частица – это перемещающаяся в пространстве и меняющий свою форму объем, содержащий в разные моменты времени одни и те же атомы и молекулы газа. Тем самым его масса постоянная. Для простоты вывода будем считать, что за короткое время куб не меняет своей формы и смещается по всем направлениям на расстояние, много меньшее его размеров.
Определим
сначала силу, действующую на куб, например
в направлении оси
.
Она, очевидно, равна разности давлений
на левой и правой границах, умноженной
на их площади (иных сил по предположению
нет):
.
Сила
равна
ускорению жидкой частицы в направлении
.
Умноженному на его массу
:
. (5)
Заменяя в правом выражении для разность давлений через производную от давления по и приравнивая его к (5), приходим к уравнению, описывающему движение газа вдоль оси :
. (6)
Точно
также получаем уравнения движения по
направлениям
:
, (7)
, (8)
имеющие как и в (6), очевидный физический смысл. В векторной форме уравнения (6) – (8) имеют вид
. (9)
Поясним,
что (6) – (9) через
обозначена
полная (субстанциональная, т.е связанная
частицами газа) производная по времени
какой-либо величины, характеризующей
данную неизменную массу газа.
Раскрыв
через
частные производные по
и
в
соответствии с правилом
,
придем к уравнениям
движения Эйлера
. (10)
Будучи записаны покоординатно, они принимают вид
, (11)
, (12)
. (13)
В
отличие от течения грунтовых вод,
градиенты давления в уравнениях газа
(6) – (13) определяют компоненты ускорения
вещества, а не компоненты его скорости
(сравнение с законом Дарси). Уравнения
(4), (11) – (13) содержат пять неизвестных
величин -
.
Для их замыкания естественно использовать
закон сохранения энергии.
3. Уравнение энергии.
Для его получения используем ту же упрощенную схему, что и для уравнений движения газа: будем рассматривать изменение внутренней энергии фиксированной массы газа за короткий промежуток времени . Так как по сделанным допущениям в веществе отсутствует теплопроводность, вязкость и источники (стоки) энергии, то это изменение вызывается лишь работой сил давления на гранях куба при его сжатии или расширении. Работа давления, связанная с движением граней объема вдоль оси , очевидно, равна
,
где
слагаемые в скобках можно, отбрасывая
члены второго порядка малости, переписать
через производную
и
получить
.
Здесь – среднее давление в элементарном объеме. Аналогично
,
.
Полная работа, совершенная над газом за время , есть
.
Она равна изменению внутренней энергии объема, т.е.
,
-
удельная внутренняя энергия. Приравняв
оба выражения для
и устремив к нулю
,
окончательно получим
, (14)
где
- полная (субстанциональная) производная
внутренней энергии по времени. Заметим,
что с помощью новых уравнений (14)
приводится, подобно (4), к дивергентному
виду
. (15)
Слева в (15) стоит производная от полной (внутренней и кинетической) энергии газа в данной точке пространства. Так как термодинамические свойства вещества предполагаются известными, то - известная функция уже введенных величин и , и уравнение (14) либо (15) дает недостающую связь для определения искомых газодинамических величин.
Лекция№4.