Совместное применение нескольких фундаментальных законов
1. Предварительные понятия газовой динамики.
Заметное изменение плотностей жидкостей и твердых тел может достигаться лишь при огромных давлениях в десятки и сотни тысяч атмосфер и выше. Газообразные среды гораздо легче подвергаются сжатию: при перепаде давления в одну атмосферу плотность газа, первоначально находившегося при атмосферном давлении, уменьшается или увеличивается на величину, сопоставимую с начальной его плотностью.
В газовой динамике, изучающей движение сжимаемых сред под действием каких-либо внешних сил или сил давления самого вещества, считается выполненным неравенство , где - длина свободного пробега, - характерные размеры области рассматриваемого течения (сплошная среда). Считается также выполненной гипотеза о ЛТР.
В
условиях ЛТР сжимаемую среду можно
рассматривать как совокупность большого
числа жидких частиц, с размерами, много
большими
,
но много меньшими, чем
.
Для каждой такой частицы, связанной с
небольшой фиксированной массой среды,
вводятся характеризующие ее средние
величины – плотность
,
давление
,
температура
,
внутренняя энергия
и
т.д., а также скорость
ее
макроскопического движения как единого
целого. Все эти величины в общем случае
зависят от трех пространственных
переменных
и
времени
.
В дальнейшем будем также предполагать
отсутствие в среде процессов теплопередачи,
вязкого трения, источников и стоков
энергии, например, излучения, и, кроме
того, отсутствие внешних объемных сил
и источников (стоков) массы в веществе.
2. Уравнение неразрывности для сжимаемого газа.
Применим
рассуждения, аналогичные тем, которые
использовались для вывода уравнений
неразрывности для течения грунтовых
вод и процесса теплопередачи. Рассмотрим
в некоторой области пространства,
занятой движущимся газом, элементарным
кубом со сторонами
и
подсчитаем в нем баланс массы за время
(рис. 2.1).
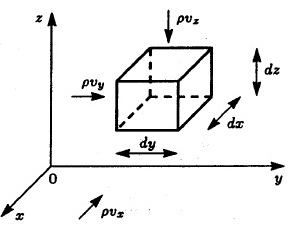
Рис. 2.1
Здесь
–
компоненты скорости по соответствующим
осям. По оси
через
грань с координатой
в
кубик за время
поступает
масса газа, равная
,
поскольку
величина
ничто
иное, как поток массы по направлению
оси
.
За то же самое время из грани с координатой
вытекает
масса
,
где
через
обозначено
приращение потока массы при переходе
от координаты
к
координате
.
Суммируя оба последних выражения и
учитывая, что
,
получаем величину изменения массы в кубе за время благодаря движению газа вдоль оси :
. (1)
Таким
же образом находим изменения массы за
счет движения по осям
:
,
. (2)
В фиксированном объеме куба изменение находящейся в нем массы газа выражается также через изменение его плотности со временем:
. (3)
Суммируя
и
приравнивая результат к
,
получаем из (1) – (3) искомое уравнение
неразрывности
, (4)
выражающее закон сохранения массы вещества применительно к движению сжимающегося газа. По своей форме и смыслу (скорость изменения величины определяется дивергенцией потока этой величины) оно вполне аналогично уравнению неразрывностью. Однако аналогия с течением грунтовых вод на этом заканчивается. При свободном движении газа его динамика определяется лишь силами давления самого газа, в отличие от движения жидкости, испытывающей сопротивление сил грунта.