Вариационные принципы и математические модели
Общая схема принципа Гамильтона.
Пусть
имеется механическая система, формального
или строгого определения которой пока
давать не будем, имея в виду, что все
взаимодействия между элементами такой
системы определяются законами механики
(один из простейших примеров, система
«шарик – пружина»). Ведем понятие
обобщенных
координат
,
полностью определяющих положение
механической системы в пространстве.
Величина
может
быть декартовой координатой (например,
координата
в
системе «шарик – пружина»), радиусом-вектором,
угловой координатой, набором координат
материальных точек, составляющих систему
и т.д. Величину
естественно
называть обобщенной
скоростью
механической системы в момент времени
.
Набор величин
и
определяет
состояние механической системы во все
моменты времени.
Для описания механической системы вводится функция Лагранжа, которая, в простейших случаях, имеет явный смысл и записывается в следующем виде
, (1)
где
и
-
кинетическая и потенциальная энергии
соответственно.
Введем
величину
,
называемой действием:
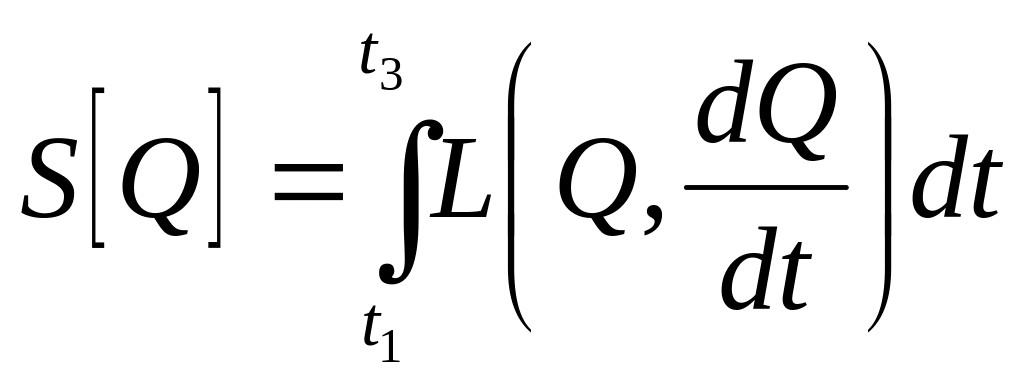. (2)
Интеграл
(2), очевидно, является функционалом от
обобщенной координаты
,
т.е. функции
,
заданной на отрезке
,
он ставит в соответствие некоторое
число
(действие).
Принцип Гамильтона для механической системы гласит: если система движется по законам механики, то - стационарная функция для , или
. (3)
Фигурирующая
в принципе
наименьшего действия
(3) функция
-
некоторая пробная функция, обращающаяся
в ноль, в моменты
и
удовлетворяющая тому условию, что
-
возможная координата данной системы
(в остальном
произвольна).
Смысл
принципа (3) в том, что из всех априори
мыслимых (допускаемых) траекторий
(движений) системы между моментами
выбирается
(реализуется) движение, доставляющее
минимум функционалу действие (отсюда
и происходит название принципа). Функция
называется
вариацией
величины
.
Итак,
схема применения принципы Гамильтона
(3) для построения моделей механических
систем состоит в следующем: определяются
обобщенные координаты
и
обобщенные скорости
системы,
строятся функция Лагранжа
и
функционал действия
,
минимизация которого на вариациях
координаты
и
дает искомую модель.
2. Предварительные сведения о процессах теплопередачи.
Тепловая
энергия
или тепло
– это энергия хаотичного движения
атомов или молекул вещества. Обмен
теплом между различными участками
называется теплопередачей,
а сами материалы, обладающие хорошо
выраженным свойством теплопередачи, -
теплопроводными.
К ним относятся, например, металлы, в
которых тепловая энергия переносится
в основном свободными электронами,
некоторыми газами и т.д. Процессы передачи
тепла рассматриваются в условиях так
называемого локального
термодинамического равновесия
(ЛТР). Понятие ЛТР для газов вводится
при
,
т.е. когда длина свободного пробега
частиц вещества много меньше характерных
размеров рассматриваемого объекта
(сплошная
среда).
ЛТР подразумевает также, что процессы
изучаются при временах, больше чем
(время между столкновениями частиц), и
на размерах, больших, чем
.
Тогда в областях вещества, размеры
которых превосходят величину
(но много меньше величины
),
устанавливается равновесие и для них
можно ввести средние величины плотности,
скорости теплового движения частиц и
т.д.
Эти локальные величины (разные в разных точках среды) при сформулированных предположениях находятся из равновесного максвелловского распределения частиц. К ним относится температура , определяющая среднюю кинетическую энергию частиц:
,
где
–
масса частицы,
- средняя скорость хаотичного движения,
- постоянная Больцмана (в случае так
называемого больцмановского газа).
Связанная
с хаотичным движением частиц энергии
вещества (внутренняя энергия) определяется
через температуру с помощью величины
удельной теплоемкости
,
а именно
,
,
где
–
плотность вещества (
-
число частиц в единице объема),
-
внутренняя
энергия единицы массы.
Другими словами, теплоемкость – это
энергия, которую необходимо сообщить
единице массы вещества, чтобы увеличить
температуру на один градус.
Наиболее
простое выражение для теплоемкости
получается в случае идеального газа
(газа, частицы которого взаимодействуют
лишь при непосредственном взаимодействии
столкновения и, подобно биллиардным
шарам, без потери суммарной кинетической
энергии). Если в некотором объеме
идеального газа содержится
частиц,
то их полная внутренняя энергия есть
,
где
-
суммарная масса частиц, а удельная
внутренняя энергия, или энергия на
единицу массы, дается формулой
,
Т.е.
теплоемкость идеального газа равна
и
не зависит от величин
.
В общем случае связь между внутренней
энергией и температурой более сложная.
Например, помимо кинетической энергии
движущихся частиц, внутренняя энергия
содержит составляющую, связанную с
потенциальной энергией их взаимодействия,
зависящей от среднего расстояния
между
ними. В свою очередь
,
где
-
число частиц в единице объема, т.е.
зависит от плотности
.
Поэтому в теории теплопередачи величины
(или, что то же самое,
)
являются, вообще говоря, функциями от
и
.
Их конкретный вид определяется свойствами
рассматриваемой среды.