Термодинамика

1. Динамический метод основан на законах Ньютона,под состоянием частицы определяется знание ее координат и импульсов

Термодинамический метод возник в след за динамическим. Вообще говоря, в любой системе можно рассмотреть или заметить те состояния,которые связаны с микросостояниями.

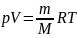
Связывает параметры уравнения состояния,макропараметры

Если число частиц в системе достаточно весомо,то термодинамический метод применить нельзя.

Статистический метод -этот метод основан на том, что свойства макроскопической системы в конеч­ном счете определяются свойствами частиц системы, особенностями их движения и усредненными значениями динамических характеристик этих частиц (скорости, энер­гии и т. д.). Например, температура тела определяется скоростью хаотического движе­ния его молекул, но так как в любой момент времени разные молекулы имеют различные скорости, то она может быть выражена только через среднее значение скорости движения молекул. Нельзя говорить о температуре одной молекулы. Таким образом, макроскопические характеристики тел имеют физический смысл лишь в слу­чае большого числа молекул.

Параметры состояния – свойства системы, выбранные в качестве независимых переменных. 

Функция состояния – величина, определяемая этими параметрами, однозначно характеризует систему и не зависит от пути ее перехода из одного состояния в другое. (если для 1 моля идеального газа параметрами состояния выбрать давление и температуру, то функцию состояния объем можно рассчитать по ура нению состояния Менделеева-Клапейрона РV=RТ).

Способ распределения частиц по ячейкам без учета их номеров называется макросостоянием системы.

(В рассматриваемом примере возможны всего пять разных макросостояний . 1 – все четыре частицы находятся в левой ячейке, 2 – три частицы в левой ячейке и одна в правой, 3 – две частицы в левой ячейке и две в правой. Ещё два макросостояния симметричны первому и второму.)

 

Способ распределения частиц по ячейкам с учетом их номеров называется микросостоянием системы. 

Число микросостояний, соответствующих какому-либо макросостоянию системы, называется термодинамической вероятностью(статистическим весом) этого макросостояния. Термодинамическая вероятность любого макросостояния системы не зависит от предшествующих и будущих состояний. Изменение термодинамической вероятности при переходе от одного макросостояния к другому не зависит от пути перехода, а зависит только от начального и конечного макросостояний. При циклическом процессе термодинамическая вероятность возвращается к исходному значению.

Энтропия в статистической физике Приведенное количество теплоты, которое сообщается телу на малом участке процесса, равно δQ/T. Приведенное количество теплоты, которое сообщается телу в любом обратимом круговом процессе, равно нулю:   (1)  Из равенства нулю интеграла (1), взятого по замкнутому контуру, следует, что подынтегральное выражение δQ/T есть полный дифференциал некоторой функции, которая определяется только состоянием системы и не зависит от пути, которым система пришла в это состояние. Таким образом,   (2)  Функция состояния, у которой дифференциал равен δQ/T, называется энтропией и обозначается S.  Из формулы (1) следует, что для обратимых процессов изменение энтропии   (3)  В термодинамике доказывается, что энтропия системы, совершающей необратимый цикл, возрастает:  (4)  Выражения (3) и (4) применяются только к замкнутым системам, если же система обменивается теплотой с внешней средой, то ее энтропия может вести себя произвольным образом. Соотношения (3) и (4) можно представить в виде неравенства Клаузиуса  (5)  т. е. энтропия замкнутой системы может либо возрастать (в случае необратимых процессов), либо оставаться постоянной (в случае обратимых процессов). 

Вопрос 2

Первое начало термодинамики : количество теплоты Q, сообщенное системе, расходуется на увеличение  ее внутренней энергии  dU и на совершение работы А системой, т.е.  Q = dU + А 

Уравнение состояния идеального газа

Т=const

Работа

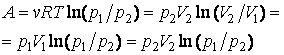
Внутренняя энергия

Теплоемкость

  Количество теплоты, котоpое нужно сообщить телу, чтобы повысить его темпеpатуpу на 1 К, называется теплоемкостью тела

В изотермическом процессе постоянна температура, то есть  . При изменении объема газу передается (или отбирается) некоторое количество тепла. Следовательно, теплоемкость идеального газа стремится к бесконечности: 

Вопрос 3

V=const

Работа A=0

Внутренняя энергия

где   — молярная теплоёмкость при постоянном объёме.

Темлоемксоть

где i — число степеней свободы частиц газа.

Вопрос 4

P=const

Работа A = p(V2 – V1) = pΔV.,площадь фигуры под графиком

Внутренняя энергия

Теплоемкость C_P=δQ/νΔT=C_V+R=((i+2)/2)*R

Вопрос 5

Изобарная теплоемкость

Изохорная теплоемкость

Уравнение Майера

,

где   — универсальная газовая постоянная,   — молярная теплоёмкость при постоянном давлении,   — молярная теплоёмкость при постоянном объёме.

Уравнение Майера вытекает из первого начала термодинамики, примененного к изобарическому процессу в идеальном газе:

,

в рассматриваемом случае:

.

Очевидно, уравнение Майера показывает, что различие теплоёмкостей газа равно работе, совершаемой одним молем идеального газа при изменении его температуры на 1 K, и разъясняет смысл универсальной газовой постоянной R — механический эквивалент теплоты.

Вопрос 6

Адиабатны процесс

Q=0,система не получает тепло

    

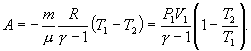
Теплоемкоcть

Уравнение Пуассона

Для идеальных газов, чью теплоёмкость можно считать постоянной, адиабата имеет простейший вид и определяется уравнением

где   — его объём,   — показатель адиабаты,   и   — теплоёмкости газа соответственно при постоянном давлении и постоянном объёме.

С учётом уравнения состояния идеального газа уравнение адиабаты может быть преобразовано к виду

где T — абсолютная температура газа. Или к виду

Поскольку   всегда больше 1, из последнего уравнения следует, что при адиабатическом сжатии (то есть при уменьшении V) газ нагревается (T возрастает), а при расширении — охлаждается, что всегда верно и для реальных газов. Нагревание при сжатии больше для того газа, у которого больше коэффициент  .

Вопрос 7

Политропный процесс проходит при постоянной теплоемкости

С=0

pVⁿ = const уравнение политропы

 называется показателем политропы.

В зависимости от процесса можно определить значение n:

1. Изотермический процесс: n = 1, так как PV¹ = const, значит PV = const, значит T = const.

2. Изобарный процесс: n = 0, так как PV⁰ = P = const.

3. Адиабатный процесс: n = γ, это следует из уравнения Пуассона.

Здесь γ — показатель адиабаты.

4. Изохорный процесс:  , так как  , значит P₁ / P₂ = (V₂ / V₁)ⁿ, значит V₂ / V₁ = (P₁ / P₂)^{(1 / n)}, значит, чтобы V₂ / V₁ обратились в 1, n должна быть бесконечность.

Работа политропного процесса

A=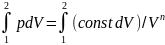

Процессы с отрицательной теплоемкостью

Однако теплоемкость может быть и отрицательной .

1) при получении тепла система охлаждается ,

2) при отдаче тепла система разогревается .

Оба случая легко объясняются при помощи первого закона термодинамики , записанного в следующем виде:

(4.4.18)

В первом случае газ производит работу расширения   в количестве большем, чем количество теплоты  , которое подводится к газу в процессе расширения   . В этом случае на производство работы помимо тепла, подведенного к газу, расходуется и некоторое количество его внутренней энергии. Хотя к газу и подводится тепло, но оно целиком превращается в работу, а убыль внутренней энергии   газа ведет к снижению температуры.

Во втором случае работа, производимая над газом при его сжатии   , оказывается по абсолютной величине большей, чем количество отдаваемого им тепла . С учетом знаков количества теплоты   и работы   равенство (4.4.19) принимает вид:

(4.4.19)

Внутренняя энергия системы увеличивается , а значит, ее температура растет, несмотря на то, что газ отдает теплоту. Подобный процесс происходит в некоторых звездах: гравитационные силы при сжатии звезды совершают работу большую, чем излучаемое ей тепло, поэтому звезда разогревается, несмотря на то, что она излучает теплоту.