11. Силы в механике (упругости, трения, тяготения).

В классической механике рассматривается три силы: упругости, трения и тяготения.

1. Сила упругости – сила, возникающая при упругой деформации тела и направленная противоположно направлению смещения частиц при деформации.

Деформация – изменение размеров и формы тела.

Упругая деформация возникает, если после прекращения действия силы деформация исчезает.

Закон Гука – сила упругости, возникающая вследствие растяжения (или сжатия), пропорциональна изменению длины деформируемого тела и направлена в сторону, противоположную смещению частиц тела при его деформации:

Где х – удлинение (сжатие) тела, коэффициент k называют коэффициентом жесткости (жесткостью). k выражается в ньютонах на метр.

Сила реакции опоры 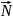– сила упругости, действующая на тело со стороны опоры (или подвеса) перпендикулярно её поверхности.

2. Сила трения – тангенциальная сила, возникающая при соприкосновении поверхностей тел и препятствующая их относительному перемещению.

Трение покоя – трение при отсутствии относительного перемещения соприкасающихся тел.

Внешнее трение (трение, возникающее в плоскости касания двух соприкасающихся тел при их относительном перемещении) бывает двух видов: трение скольжения (тело скользит по поверхности опоры) и трение качения (тело катится по поверхности опоры).

Силы трения направлены по касательной к трущимся поверхностям противоположно относительной скорости перемещения.

Сила трения покоя возникает, если

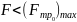
F – сила, действующая на тело, 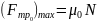, где 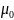– коэффициент трения покоя, N – сила реакции опоры.

Сила трения скольжения возникает, если

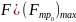
F_{тр скольж} = µ N, где µ - коэффициент трения скольжения.

3. Сила тяжести – сила, действующая на всякое тело в системе отсчёта, связанной с Землёй.

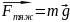
где g – ускорение свободного падения – ускорение, приобретаемое телом под действием силы тяжести.

Тяготение – универсальное взаимодействие между любыми видами материи.

Сила всемирного тяготения – сила взаимного притяжения, действующая между телами.

Закон всемирного тяготения: между любыми двумя МТ действует сила взаимного притяжения, прямо пропорциональная произведению масс этих точек и обратно пропорциональная квадрату расстояния между ними:

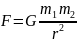
G – гравитационная постоянная, равная 6,6720*10^-11 Н*м²/кг²

Сила тяжести и сила тяготения равны между собой:

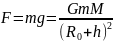
Где М – масса земли, R₀ – радиус земли, h – расстояние от поверхности земли до тела.

Отсюда 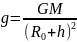, но при h≈0 , то есть все тела под действием силы тяжести независимо от их массы падают с одинаковым ускорением g (обобщённый закон Галлилея).

12. Второй закон Ньютона для вращательного движения (две формулы), момент силы, момент инерции.

Момент инерции системы (тела) относительно данной оси называют физическую величину, равную сумме произведений масс n МТ системы на квадраты их расстояний до рассматриваемой оси:

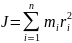
или

Момент инерции тела – мера инертности твёрдых тел при вращательном движении.

Теорема Штейнера: момент инерции тела J относительно произвольной оси равен моменту его инерции J_с относительно параллельной оси, проходящей через центр масс С тела, сложенному с произведением массы тела на квадрат расстояния а между осями:

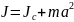
Центр масс тела (системы материальных точек) называют воображаемую точку С, положение которой характеризует распределение массы этой системы.

Момент силы относительно неподвижной точки О называют физическую величину, определяемую векторным произведением радиуса-вектора r, проведенного из точ­ки О в точку А приложения силы, на силу F

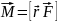
М — псевдовектор, его направление совпадает с направлением поступательного движения правого винта при его вращении от r к F. Модуль момента силы:

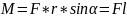
где — угол между r и F; r sin = l — кратчайшее расстояние между линией действия силы и точкой О — плечо силы.

Моментом силы относительно неподвижной оси z называется скалярная величина M_z , равная проекции на эту ось вектора М момента силы, определенного относительно произвольной точки О данной оси z

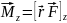
Это выражение представляет собой аналог второго закона Ньютона для вращательного движения, из которого следует, что угловое ускорение  твердого тела при вращении вокруг неподвижной оси прямо пропорционально вращающему моменту и обратно пропорционально моменту инерции относительно этой оси.

или

Момент импульса твердого тела относительно оси равен произведе­нию момента инерции тела относительно той же оси на угловую скорость.