- •III осенний семестр Лекция №1 Числовые ряды
- •Лекция №2 Сходимость положительных рядов
- •Если - сходится, то - сходится;
- •Если - расходится, то - расходится.
- •Лекция №3 Сходимость положительных рядов (продолжение)
- •Лекция №4 Сходимость положительных рядов (продолжение)
- •Ряды с членами произвольного знака
- •Лекция №5 Ряды вида
- •Лекция №6 Перестановки числовых рядов
- •Лекция №6 Перестановки числовых рядов (продолжение)
- •Лекция №8 Умножение рядов (продолжение)
- •Двойные ряды
- •Лекция №9 Двойные ряды (продолжение)
- •Бесконечные произведения
- •Лекция №10 Бесконечные произведения (продолжение)
- •Лекция №11 Функции, представляющиеся в виде бесконечных произведений
- •Функциональные последовательности и ряды
- •Лекция №12 Функциональные последовательности и ряды (продолжение)
- •Лекция №13 Функциональные последовательности и ряды (продолжение)
- •Лекция №14 Свойства предельной функции и сумма функционального ряда в случае равномерной сходимости
- •Лекция №15 Пространства и сходимость в них
- •Степенные ряды
- •Лекция №16 Степенные ряды (продолжение)
- •Лекция №17 Разложение функций в степенные ряды
- •Лекция №18 Ряды Фурье
- •Лекция №19 Ряды Фурье (продолжение)
- •Лекция №20-21 Ряды Фурье (продолжение)
- •Лекция №22 Ряды Фурье (продолжение)
- •Лекция №23 Ряды Фурье (продолжение)
- •Лекция №24 Ряды Фурье (продолжение)
- •Лекция №25 Ряды Фурье (продолжение).
- •Лекция №26 Поточечная сходимость тригонометрического ряда Фурье
- •Лекция №27 Поточечная сходимость тригонометрического ряда Фурье (продолжение)
- •Лекция №28 Собственные интегралы, зависящие от параметра
- •Лекция №30 Свойства несобственных интегралов, зависящих от параметра
- •Свойства гамма-функции
- •Лекция№31 Преобразование Фурье
- •Критерий сходимости положительного ряда.
Лекция №26 Поточечная сходимость тригонометрического ряда Фурье
Можно показать, что для тригонометрических рядов Фурье непрерывных функций отсутствует не только равномерная сходимость, но и поточечная сходимость в отдельных точках.
Теорема. Для
любой кусочно-непрерывно-дифференцируемой
функции f(x)
её тригонометрический ряд Фурье сходится
всюду, причём к f(x),
если
![]() точка
непрерывности, и к
точка
непрерывности, и к
![]() если
точка
разрыва.
если
точка
разрыва.

К доказательству этой теоремы предпошлём глубокий анализ поведения частичной суммы ряда Фурье

Этот анализ будет основываться на следующей лемме.
Лемма.
![]() новая
функция
новая
функция
![]()
![]()
Доказательство.
Отсюда для
равномерной сходимости достаточно
показать, что следующие последовательности
![]() стремятся
к нулю.
стремятся
к нулю.
При доказательстве замкнутости тригонометрической системы было установлено, что
 Это
и означает, что
Это
и означает, что

Доказано.
Лекция №27 Поточечная сходимость тригонометрического ряда Фурье (продолжение)
Укажем более простой вид частичной суммы ряда Фурье:


![]() непрерывна
на
непрерывна
на
![]()
![]() поэтому
по лемме получаем
поэтому
по лемме получаем

Далее



Итак,
![]()
Последняя запись частичной суммы Фурье называется принципом локализации Римана, согласно которому, сходимость ряда Фурье в точке зависит от значений функции в достаточно маленькой окрестности точки.
Если
![]() то
то

Покажем, используя (*), что если точка разрыва первого рода, то
![]()

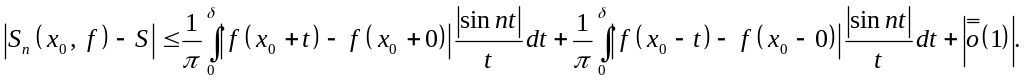
По формуле Лагранжа
![]()
Аналогично:
![]()
![]() и
для этого
и
для этого
![]() т.к.
т.к.
![]() т.е.
т.е.
![]()
Лекция №28 Собственные интегралы, зависящие от параметра
Пусть
![]() и
и
![]() тогда
определена новая функция
тогда
определена новая функция
![]()
![]() собственный
интеграл,
зависящий от параметра у.
собственный
интеграл,
зависящий от параметра у.
Необходимо
охарактеризовать свойства функции
![]() в
зависимости от свойств функции
в
зависимости от свойств функции
![]()
Теорема 1. Если
![]() то
то
![]()
Доказательство.
![]() равномерно
непрерывна на D
и
равномерно
непрерывна на D
и
![]()

![]() равномерно
непрерывна на
равномерно
непрерывна на
![]()
Доказано.
Теорема 2. Если
то![]() и
и

 повторный
интеграл.
повторный
интеграл.
Доказательство.
Пусть
 Докажем,
что
Докажем,
что
![]()

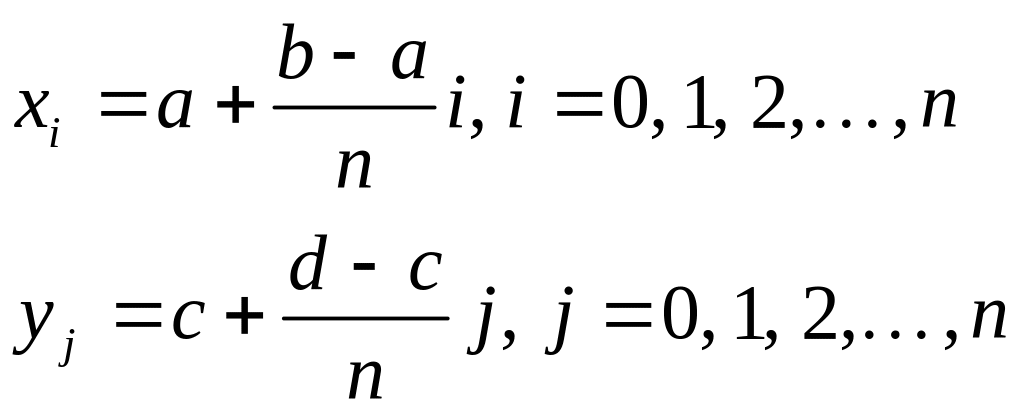
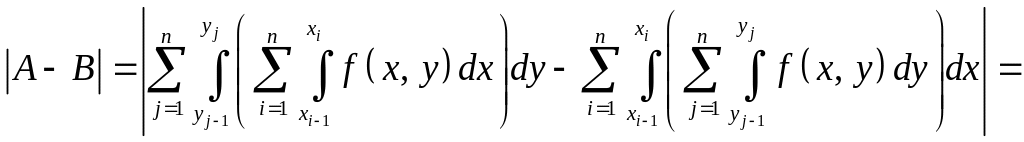 (к
каждому интегралу применим теорему о
среднем:
(к
каждому интегралу применим теорему о
среднем:
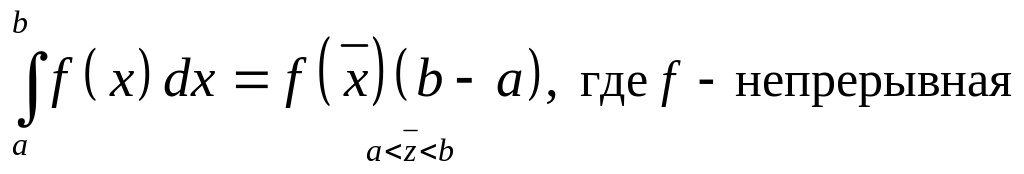 )
=
)
=

Т.к.
![]() то
в силу равномерной непрерывности
то
в силу равномерной непрерывности
![]() на
D
на
D
![]() и
и
![]()
Доказано.
Теорема 3. Если


Замечание.


Доказательство.

![]()
![]() или
или
![]() или
или
![]()
![]() и
и

Доказано.
Несобственный
интеграл –
это интеграл вида
![]()
Несобственные интегралы, зависящие от параметра

![]() несобственный
интеграл
несобственный
интеграл
![]() сходится,
когда определена функция
сходится,
когда определена функция
![]()
![]() несобственный
интеграл, зависящий от параметра.
несобственный
интеграл, зависящий от параметра.
Сходимость несобственного интеграла означает существование предела
![]() Для
определения предела существуют два
эквивалентных подхода:
Для
определения предела существуют два
эквивалентных подхода:
определение предела по Коши:

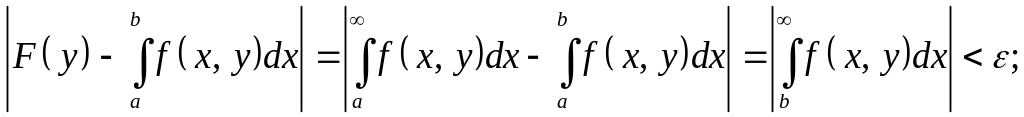
определение предела по Гейне:


Лекция №29
Несобственные интегралы, зависящие от параметра
(продолжение)
Определим условие
поточечной сходимости интеграла на
отрезке
![]()

Дадим определение равномерной сходимости.
Несобственный
интеграл
![]() сходится
равномерно на отрезке
сходится
равномерно на отрезке
![]() (по
Коши)
(по
Коши)

 т.е.
т.е.
![]() (по
Гейне)
(по
Гейне)![]()
Критерий Коши:
сходится
равномерно на отрезке
![]()
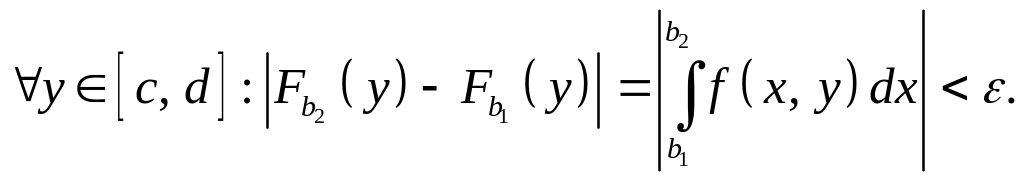
Признак равномерной сходимости Вейерштрасса:
если
![]() мажоранта
функции f
по у,
мажоранта
функции f
по у,
![]() и
и
![]() сходится,
то
сходится,
то
![]() сходится
на
сходится
на
![]() равномерно.
равномерно.
Доказательство.
сходится
![]() (по
критерию Коши)
(по
критерию Коши)![]()

 (по
критерию Коши)
(по
критерию Коши)![]() сходится
равномерно.
сходится
равномерно.
Доказано.
Пример.
![]()
![]()
 сходится.
сходится.
Данный интеграл сходится.
Рассмотрим
равномерную сходимость интегралов вида
![]() (*)
(*)
Признак Абеля (признак равномерной сходимости).
Если


 сходится
равномерно на отрезке
сходится
равномерно на отрезке

то (*) – сходится равномерно на
Признак Дирихле.
Если:
 монотонная;
монотонная;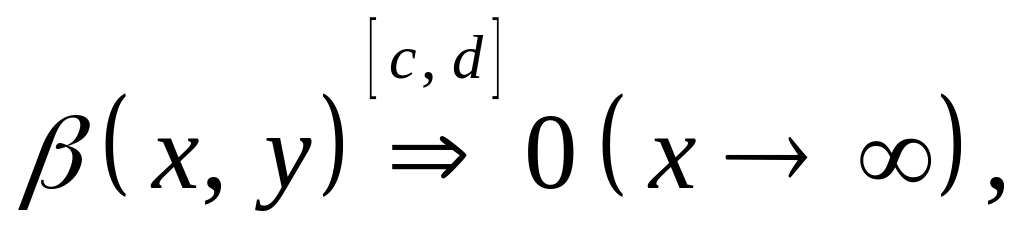 т.е.
т.е.


то (*) – сходится равномерно на отрезке
Пример. Доказать
![]() интеграл
Дирихле.
интеграл
Дирихле.
![]()
Покажем, что этот
интеграл сходится
![]() Для
этого воспользуемся признаком Дирихле:
Для
этого воспользуемся признаком Дирихле:
![]() равномерно
по y.
равномерно
по y.
 продифференцируем
по х
продифференцируем
по х



Интеграл сходится равномерно для всех у, т.к. интеграл ограничен константой.
Найдем производную


![]()
Далее покажем, что
дифференцирование под знаком интеграла
возможно, если интеграл от производной
сходится равномерно, т.е. равномерно
сходится интеграл
![]() По
признаку Вейерштрасса
По
признаку Вейерштрасса
![]()
 сходится,
сходится,