
4. Системы линейных уравнений
Общий вид системы
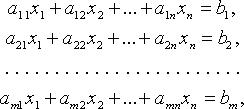
![]() , i
= 1, 2, ..., m; j
= 1, 2, ..., n,
- коэффициенты системы;
, i
= 1, 2, ..., m; j
= 1, 2, ..., n,
- коэффициенты системы; ![]() -
свободные члены;
-
свободные члены; ![]() -
переменные;
-
переменные; ![]()
Если все = 0, система называется однородной.
А) Пусть detA≠0, тогда для существует единственная обратная матрица A-1. Решение системы уравнений, записанной в матричной форме AX=B можно найти по следующей формуле X=A-1·B Пример 2.
Решить
систему уравнений матричным методом:

имеем:

обратная
матрица

Находим:
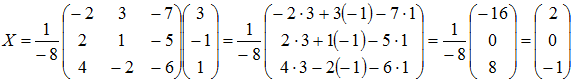 ,
т.е.
x=2; y=0; z=-1 - решение данной системы.
,
т.е.
x=2; y=0; z=-1 - решение данной системы.
б)

В) Процесс решения системы линейных уравнений
(2)
![]()
по методу Гаусса состоит из 2х этапов:
Прямой ход
Система (2) приводится к треугольному виду
1.
Предполагаем, что ![]() .
Тогда первое уравнение системы (2) делим
на коэффициент
.
Тогда первое уравнение системы (2) делим
на коэффициент ![]() ,
в результате получаем уравнение
,
в результате получаем уравнение
![]()
.
Затем
из каждого из оставшихся уравнений
вычитается первое, умноженное на
соответствующий коэффициент ![]() .
В результате система преобразуются к
виду:
.
В результате система преобразуются к
виду:
2.
В предположении, что ![]() ,
делим второе уравнение на коэффициент
,
делим второе уравнение на коэффициент ![]() и
исключаем неизвестное
и
исключаем неизвестное ![]() из
всех последующих уравнений и т.д.
из
всех последующих уравнений и т.д.
3. Получаем систему уравнений с треугольной матрицей:
(3)
Обратный ход
Непосредственное определение неизвестных
1.
Из ![]() го
уравнения системы (3) определяем
го
уравнения системы (3) определяем ![]()
2.
Из ![]() го
- определяем
го
- определяем ![]() и
т.д.
и
т.д.
5. Однородные системы линейных уравнений
Однородная система линейных уравнений AX = 0 всегда совместна. Она имеет нетривиальные (ненулевые) решения, если r = rank A < n.
Для однородных систем базисные переменные (коэффициенты при которых образуют базисный минор) выражаются через свободные переменные соотношениями вида:

Тогда n - r линейно независимыми вектор-решениями будут:
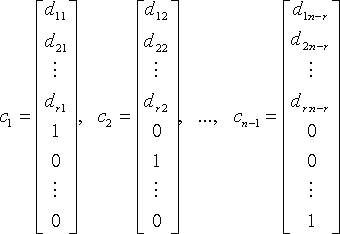
а
любое другое решение является их линейной
комбинацией. Вектор-решения ![]() образуют
нормированную фундаментальную систему.
образуют
нормированную фундаментальную систему.
В
линейном пространстве ![]() множество
решений однородной системы линейных
уравнений образует подпространство
размерности n
- r;
-
базис этого подпространства.
множество
решений однородной системы линейных
уравнений образует подпространство
размерности n
- r;
-
базис этого подпространства.
Матрица как запись коэффициентов системы линейных уравнений
Систему из m уравнений с n неизвестными
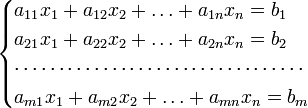
можно представить в матричном виде
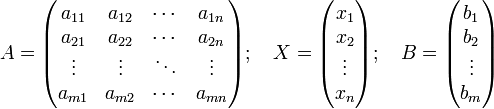
и тогда всю систему можно записать так:
AX = B,
где A имеет смысл таблицы коэффициентов aij системы уравнений.
Если m = n и матрица A невырожденная, то решение этого уравнения состоит в нахождении обратной матрицы A − 1, поскольку умножив обе части уравнения на эту матрицу слева
A − 1AX = A − 1B
A − 1A — превращается в E (единичную матрицу). И это даёт возможность получить столбец корней уравнений
X = A − 1B.
Все правила, по которым проводятся операции над матрицами, выводятся из операций над системами уравнений.
