
Ма́трица — математический объект, записываемый в виде прямоугольной таблицы элементов кольца или поля (например, целых или комплексных чисел), которая представляет собой совокупностьстрок и столбцов, на пересечении которых находятся её элементы. Количество строк и столбцов матрицы задают размер матрицы. Хотя исторически рассматривались, например, треугольные матрицы, в настоящее время говорят исключительно о матрицах прямоугольной формы, так как они являются наиболее удобными и общими.
Операции над матрицами
Умножение матрицы на число
Умножение матрицы A на число λ (обозначение: λA) заключается в построении матрицы B, элементы которой получены путём умножения каждого элемента матрицы A на это число, то есть каждый элемент матрицы B равен
![]()
Свойства умножения матриц на число
1. 1*A = A;
2. (Λβ)A = Λ(βA)
3. (Λ+β)A = ΛA + βA
4. Λ(A+B) = ΛA + ΛB
Сложение матриц
Сложение матриц A + B есть операция нахождения матрицы C, все элементы которой равны попарной сумме всех соответствующих элементов матриц A и B, то есть каждый элемент матрицы C равен
![]()
Свойства сложения матриц
5.коммутативность;
6.ассоциативность;
7.сложение с нулевой матрицей;
8.существование противоположной матрицы;
Все свойства линейных операций повторяют аксиомы линейного пространства и поэтому справедлива теорема:
Множество всех матриц одинаковых размеров MxN образуют линейное пространство над полем P(полем всех действительных или комплексных чисел), поэтому каждая матрица является и вектором этого пространства.
Умножение матриц

Умножение
матриц (обозначение: AB,
реже со знаком умножения ![]() ) —
есть операция вычисления матрицы C,
элементы которой равны сумме произведений
элементов в соответствующей строке
первого множителя и столбце второго.
) —
есть операция вычисления матрицы C,
элементы которой равны сумме произведений
элементов в соответствующей строке
первого множителя и столбце второго.
![]()
Количество
столбцов в матрице A должно
совпадать с количеством строк в матрице B.
Если матрица A имеет
размерность ![]() , B —
, B — ![]() ,
то размерность их произведения AB = C есть
,
то размерность их произведения AB = C есть ![]() .
.
Свойства умножения матриц
1.Ассоциативность;
2.произведение не коммутативно;
3.произведение коммутативно в случае умножения с единичной матрицей;
4.справедливость дистрибутивного закона;
5.(ΛA)B = Λ(AB) = A(ΛB);
Комплексное сопряжение
Если
элементами матрицы A =
(aij) являются
комплексные числа, то комплексно
сопряжённая (не
путать с эрмитово
сопряжённой!
см. далее) матрица равна ![]() .
Здесь
.
Здесь ![]() —
число, комплексно
сопряжённое к a.
—
число, комплексно
сопряжённое к a.
Транспонирование и эрмитово сопряжение
Транспонирование
уже обсуждалось выше: если A =
(aij),
то AT =
(aji).
Для комплексных матриц более
употребительно эрмитово
сопряжение: ![]() .
С точки зрения операторного взгляда на
матрицы, транспонированная и эрмитово
сопряжённая матрица — это матрицы
оператора, сопряжённого относительно скалярного или эрмитова произведения,
соответственно.
.
С точки зрения операторного взгляда на
матрицы, транспонированная и эрмитово
сопряжённая матрица — это матрицы
оператора, сопряжённого относительно скалярного или эрмитова произведения,
соответственно.
Виды матриц
Введем понятие матриц: квадратных, диагональных, единичных и нулевых.
Определение матрицы квадратной: Квадратной матрицей n-го порядка называется матрица размера n×n.
В случае квадратной матрицы
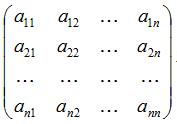
вводятся понятие главной и побочной диагоналей. Главной диагональю матрицы называется диагональ, идущая из левого верхнего угла матрицы в правый нижний ее угол.
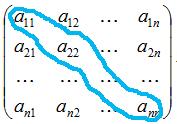
Побочной диагональю той же матрицы называется диагональ, идущая из левого нижнего угла в правый верхний угол.

Понятие диагональной матрицы: Диагональной называется квадратная матрица, у которой все элементы вне главной диагонали равны нулю.
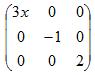
Понятие единичной матрицы: Единичной (обозначается Е иногда I) называется диагональная матрица с единицами на главной диагонали.

Понятие нулевой матрицы: Нулевой называется матрица, все элементы которой равны нулю.

Две
матрицы А и В называются равными (А=В),
если они одинакового размера (т.е. имеют
одинаковое количество строе и одинаковое
количество столбцов и их соответствующие
элементы равны). Так, если
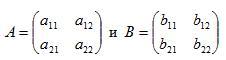 то
А=B, если a11=b11,
a12=b12,
a21=b21,
a22=b22
то
А=B, если a11=b11,
a12=b12,
a21=b21,
a22=b22
