
Файлы по мостам / расчет жб / Proektirovanie_gelezobetonnogo_GD_mosta
.pdf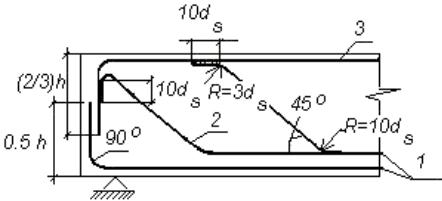
Рис. 3.7. Схема стыковки продольной отогнутой арматуры балки: 1 – продольная рабочая арматура; 2 – отогнутая арматура; 3 – арматура сжатой зоны (монтажная)
Продольную рабочую арматуру и хомуты в балках следует объединять в каркасы (см. рис. 3.6). При известных местах расположения отгибов арматуры, а также после установки минимально допустимого по нормам количества хомутов и продольной арматуры в стенке балки, необходимо проверить прочность сжатого бетона наклонных сечений по трещине прежде всего в приопорном сечении.
Согласно [2] приопорные участки балки располагаются от границ концевых участков до четверти пролета. Концевые участки балки простираются от ее конца в сторону пролета на длину, равную высоте балки h , считая от оси опорной части (см. рис. 3.5).
Как правило, рассматривается несколько возможных направлений наклонных трещин, в каждом случае определяется поперечная сила Qi в сечении у конца рассматриваемой трещины [5].
В курсовой работе расчет наклонного сечения по прочности на действие поперечной силы достаточно ограничить сечением на опоре.
Прочность сжатого бетона будет обеспечена в зоне наклонной трещины, т.е. исключено разрушение балки по схеме (см. рис. 3.4), в случае выполнения условия, при котором поперечная сила, действующая в конце наклонного сечения, не превышает значения суммарного внутреннего усилия, возникающего в отогнутой, поперечной арматуре и бетоне сжатой зоны.
Проверка прочности наклонного сечения на действие поперечной силы выполняется в соответствии с [2, пп. 3.77–3.78, с. 52–53]. Вычерчивается схема усилий в опорном сечении, наклонном к продольной оси балки (рис. 3.8).
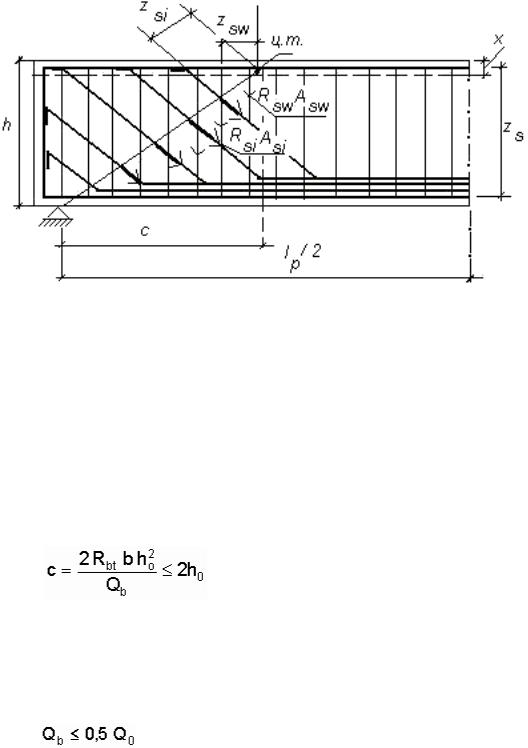
Рис. 3.8. Схема усилий в сечении, наклонном к продольной оси балки: lp – расчетная длина пролетного строения; h – высота балки; с – проекция длины наклонного сечения; zsw, zsi, zs – плечи сил в рассматриваемых стержнях арматуры; ц.т. – центр сжатой зоны в конце наклонного сечения
Для этого определяется проекция длины невыгоднейшего наклонного сечения на продольную ось балки "с" посредством сравнительных расчетов из условия минимума поперечной силы, воспринимаемой бетоном и арматурой [2, п. 3.79], по формуле
, |
(3.26) |
где Rbt – расчетное сопротивление бетона осевому растяжению, определяется по [2, табл. 23, с. 35]; Qb – поперечное усилие, передаваемое на бетон сжатой зоны над концом наклонного сечения, которое ограничивается
. |
(3.27) |
Далее на чертеже (рис. 3.8) в масштабе указывается необходимое количество стержней отогнутой арматуры с усилиями RsAsi, хомутов – RswAsw, пересекающих проекцию длины наклонного сечения "c". Центр тяжести сжатой зоны бетона находится на уровне х/2 , который отмечается в конце наклонного сечения (рис. 3.8). Затем определяются плечи усилий RsAsi и RswAsw до центра тяжести сжатой зоны zsi и zsw (рис. 3.8).
Расчет наклонного сечения на действие поперечной силы (рис. 3.8) следует производить из условия
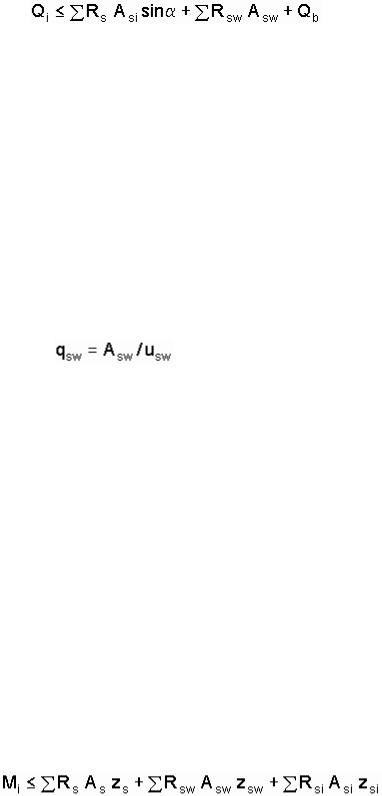
, |
(3.28) |
где Qi – поперечная сила, возникающая в конце наклонного сечения; α Rs Asi sinα , α Rsw Asw – суммы проекций усилий всех стержней пересекаемой арматуры (отогнутой и хомутов) при длине проекции сечения "с"; Rsi, Rsw – расчетные сопротивления арматуры [2, табл. 31, с. 41], определенные с учетом коэффициента условий работы man [2, п. 3.10, с. 43]; Asi, Asw – площади поперечных сечений наклонных стержней и хомутов, пересекаемых наклонным сечением балки; α – угол наклона стержней к продольной оси балки (α = 45° ).
Если условие (3.28) не выполняется, то необходимо изменить принятую ранее схему расстановки отгибов рабочей арматуры, но лучше увеличить интенсивность армирования хомутами, изменив шаг армирования. При этом можно воспользоваться формулой
, |
(3.29) |
где qsw – интенсивность армирования хомутами; Asw – требуемая площадь хомутов, пересекающих наклонное сечение балки; usw – шаг хомутов вдоль оси балки.
Расчет на действие изгибающего момента. Расчет по прочности сечения, наклонного к продольной оси балки, на действие изгибающего момента производится в соответствии с [2 , п. 3.83, с. 53–54].
Воснову расчета заложена модель, учитывающая, что при разрушении балки от действия изгибающего момента (см. рис. 3.4) прочность обеспечивается несущей способностью арматуры (рабочей продольной, отогнутой, хомутами), пересекающей наклонное сечение. На действие изгибающего момента обычно проверяются те же сечения, что и на действие поперечной силы.
Вданном случае лучше произвести расчет для сечения в четверти пролета. При этом с учетом схемы усилий в наклонном сечении (см. рис. 3.8) должно быть выполнено условие прочности:
, |
(3.30) |
где Мi – момент от расчетных нагрузок в рассматриваемом сечении (в конце наклонного сечения); zs, zsw, zsi – расстояние от усилий в рабочей, отогнутой арматуре и хомутах, пересекающих наклонное сечение, до точки приложения равнодействующей усилий в сжатой зоне бетона (см. рис. 3.8).
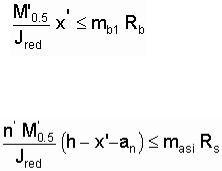
Если проверка условия (3.30) не выполняется, то необходимо увеличить площадь поперечного сечения отогнутой арматуры Аsi или ветвей хомутов Asw, пересекающих наклонное сечение.
3.1.6. Расчет на выносливость
Материал пролетного строения со временем подвергается усталостному разрушению. Бетон и арматурная сталь при возникновении в конструкциях определенного числа циклов переменных напряжений хрупко разрушается, если максимальные напряжения превысят критерий, называемый пределом выносливости [2,5]. Большое влияние на изменение напряженного состояния балок оказывает действие временной нагрузки от подвижного состава.
Согласно нормам проектирования [2] на выносливость рассчитывают только нормальные сечения. Предпосылками расчета главных балок пролетного строения на выносливость служат следующие основные понятия. В соответствии с теорией расчета железобетонных балок допускается раскрытие в них трещин в растянутой зоне [5]. При этом в бетоне и арматуре наибольшие напряжения возникают в сечении с трещиной. В основу расчета сечения балки положено также напряженное состояние, при котором с появлением и интенсивным развитием трещин в растянутой зоне бетон этой зоны из работы сечения полностью выключается, а все растягивающие усилия воспринимаются арматурой (см. рис. 3.2, г).
Расчет на выносливость балки железобетонного пролетного строения производится по формулам [2, п. 3.34, с. 56]. Расчет на выносливость включает в себя проверки изгиба в одной из главных плоскостей по бетону и арматуре. Расчет производится по характеристикам приведенного к бетону сечения, в середине балки.
При проверке напряжений рассматриваемого сечения балки должны соблюдаться условия [2]:
по бетону
; |
(3.31) |
по арматуре
, |
( 3.32) |

где  – изгибающий момент из расчета на выносливость;
– изгибающий момент из расчета на выносливость;  – момент инерции приведенного к бетону сечения относительно нейтральной оси; х' – высота сжатой зоны бетона из расчета на выносливость.
– момент инерции приведенного к бетону сечения относительно нейтральной оси; х' – высота сжатой зоны бетона из расчета на выносливость.
Для изгибаемых элементов положение нейтральной оси, проходящей через центр тяжести приведенного сечения, определяется из условия равенства нулю статического момента всего сечения по выражению [5]:
, |
(3.33) |
где – статические моменты соответственно площадей сжатой зоны бетона, сжатой и растянутой арматуры относительно нейтральной оси, которые определяются по формулам для таврового сечения:
– статические моменты соответственно площадей сжатой зоны бетона, сжатой и растянутой арматуры относительно нейтральной оси, которые определяются по формулам для таврового сечения:
 . (3.34)
. (3.34)
После решения уравнения получим значение высоты сжатой зоны бетона
. (3.35)
Приведенный момент инерции сечения при этом определится по формуле
. (3.36)
Решая аналогично для прямоугольного сечения, т.е. когда нейтральная ось проходит в пределах плиты  , получим:
, получим:
; (3.37)
 . (3.38)
. (3.38)
Правые части выражений (3.31) и (3.32) определяются согласно [2, п. 3.39,
с. 41]:
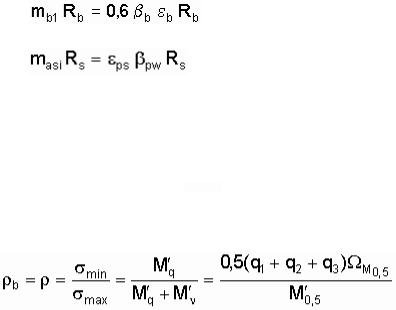
; |
(3.39) |
, |
(3.40) |
где  – коэффициенты, учитывающие рост прочности бетона во времени и условия работы арматурных элементов при наличии сварных стыков [2, пп.
– коэффициенты, учитывающие рост прочности бетона во времени и условия работы арматурных элементов при наличии сварных стыков [2, пп.
3.26, 3.39];  – коэффициенты, зависящие от асимметрии цикла
– коэффициенты, зависящие от асимметрии цикла
повторяющихся напряжений [2, пп. 3.26, 3.39], определяемые с учетом выражения (3.5) по формуле
[2, пп. 3.26, 3.39], определяемые с учетом выражения (3.5) по формуле
. (3.41)
Если при проверке напряжений в сечении балки посередине пролета по бетону условие (3.31) не выполняется, то требуется увеличить класс бетона или площадь поперечного сечения рабочей арматуры и сделать новый расчет. Если не выполняется проверка по арматуре (3.32), то необходимо увеличить класс арматуры или площадь ее поперечного сечения и сделать новый расчет. При этом в курсовой работе следует отметить, что подбор арматуры балки пролетного строения произведен из расчета на выносливость. При этом желательно произвести корректировку расчета на прочность с учетом увеличенного поперечного сечения рабочей арматуры.
3.1.7. Расчет по трещиностойкости
Расчеты по трещиностойкости относятся к расчетам по предельным состояниям второй группы. Трещиностойкость определяет долговечность пролетного строения и оказывает влияние на экономические показатели [5]. При этом решается задача о недопуске в процессе эксплуатации балки трещин, а соответственно коррозии арматуры, применении такого бетона, который препятствовал бы развитию повреждений, возникающих от неблагоприятного влияния внешней среды.
Железобетонные пролетные строения должны удовлетворять категории требований по трещиностойкости 3в [2 , табл. 39, с. 57].
Трещиностойкость характеризуется значениями растягивающих и сжимающих напряжений в бетоне, а также расчетной шириной раскрытия трещин. Согласно [2] проектирование железобетонных пролетных строений предусматривает расчеты на раскрытие нормальных и наклонных к продольной оси балки трещин.

Учитывая, что в конструкциях, проектируемых по категории требований по трещиностойкости 3в, допускается образование трещин [2, п. 3.102, с. 58], расчеты сводят к определению расчетной ширины возможного их раскрытия.
Расчет по раскрытию трещин сводится к проверке выполнения условия по ограничению ширины раскрытия трещины [2]:
, |
(3.42) |
где – расчетная ширина раскрытия трещины, см;
– расчетная ширина раскрытия трещины, см;  – допускаемая ширина раскрытия трещины в зависимости от категории требований по трещиностойкости.
– допускаемая ширина раскрытия трещины в зависимости от категории требований по трещиностойкости.
В общем случае принято, что ширина раскрытия нормальных трещин на уровне растянутой арматуры прямо пропорциональна напряжению в ней  и
и
обратно пропорциональна модулю упругости арматурной стали и определяется по формуле [2]
и определяется по формуле [2]
, |
(3.43) |
где  – напряжения в наиболее растянутых стержнях продольной арматуры, определяемые по формуле [2]:
– напряжения в наиболее растянутых стержнях продольной арматуры, определяемые по формуле [2]:
, |
(3.44) |
где х– высота сжатой зоны бетона из расчета на прочность; z – расстояние от центра тяжести площади растянутой арматуры до точки приложения
равнодействующей усилий в сжатой зоне бетона ( );
);  – расстояние от наиболее растянутой грани сечения балки до оси ближайшего (нижнего) ряда рабочей арматуры; ψ – коэффициент раскрытия трещин, определяемый для арматуры периодического профиля
– расстояние от наиболее растянутой грани сечения балки до оси ближайшего (нижнего) ряда рабочей арматуры; ψ – коэффициент раскрытия трещин, определяемый для арматуры периодического профиля
, |
(3.45) |
где  – радиус армирования, определяемый при раскрытии нормальных трещин по формуле [2]
– радиус армирования, определяемый при раскрытии нормальных трещин по формуле [2]
, |
(3.46) |
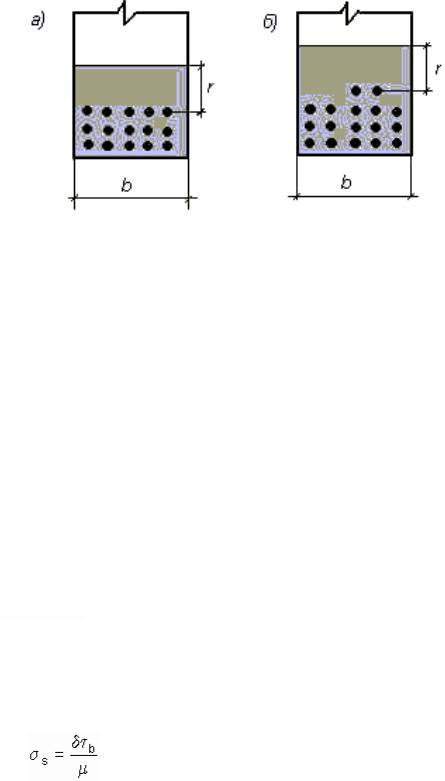
где Ar – площадь зоны взаимодействия арматуры с бетоном, определяемая с учетом геометрических параметров балки и ограниченная радиусом
взаимодействия (рис. 3.9).
(рис. 3.9).
Рис. 3.9. Варианты армирования железобетонной балки: b – ширина ребра; r – радиус армирования
Ar ограничивается контуром сечения балки и горизонтальной линией, проведенной параллельно нейтральной оси на расстоянии r от ближайшего к ней ряда рабочих стержней арматуры (рис. 3.9, а). Если площадь сечения арматурных стержней в этом ряду меньше половины площади арматуры предыдущего ряда, то расстояние до границы зоны взаимодействия арматуры с бетоном измеряется от оси предыдущего ряда (рис. 3.9, б).
Необходимо обратить внимание на то, что зона взаимодействия должна располагаться в пределах растянутой части сечения, т.е. ее граница не должна выходить за нейтральную ось.
Проверка по ограничению ширины раскрытия наклонных трещин осуществляется для центра тяжести приведенного сечения [5].
Ширина раскрытия наклонных трещин в железобетонных балках определяется по формуле (3.42) при ограничении расчетной ширины
раскрытия см.
см.
Напряжения  в отгибах, хомутах и продольной арматуре ребер определяются по формуле [2, п. 3.107]
в отгибах, хомутах и продольной арматуре ребер определяются по формуле [2, п. 3.107]
, |
(3.47) |
где  – коэффициент, учитывающий перераспределения напряжений в зоне образования наклонных трещин, определяемый по формуле
– коэффициент, учитывающий перераспределения напряжений в зоне образования наклонных трещин, определяемый по формуле

, |
(3.48) |
где  – длина наклонной трещины, см.
– длина наклонной трещины, см.
Учитывая, что в балках из обычного железобетона на уровне оси, проходящей через центр тяжести приведенного сечения, нормальные напряжения на вертикальной и горизонтальной плоскостях сечения равны нулю, следовательно, допускается наклонную (предполагаемую) трещину принимать направленной под углом 45о к оси балки (рис. 3.10);  – коэффициент армирования стенки балки на участке наклонной трещины, определяемый по формуле [5]
– коэффициент армирования стенки балки на участке наклонной трещины, определяемый по формуле [5]
|
, |
(3.49) |
где  – соответственно площадь одного отогнутого стержня, одной
– соответственно площадь одного отогнутого стержня, одной
ветви хомута, одного продольного стержня (рис. 3.10);  – углы наклона отгибов, хомутов, продольных стержней к рассчитываемому сечению
– углы наклона отгибов, хомутов, продольных стержней к рассчитываемому сечению
(рис. 3.10, а);  – ширина ребра на уровне центра тяжести сечения;
– ширина ребра на уровне центра тяжести сечения;  – длина предполагаемой наклонной трещины (измеряется от ближайшего от нейтральной оси ряда растянутой рабочей арматуры до начала вута верхнего пояса).
– длина предполагаемой наклонной трещины (измеряется от ближайшего от нейтральной оси ряда растянутой рабочей арматуры до начала вута верхнего пояса).
Направление наклонной трещины принимается перпендикулярным главным растягивающим напряжениям в центре тяжести приведенного сечения;
 – касательные напряжения в бетоне стенки, вызываемые действием поперечной силы и кручением, которые снижают трещиностойкость балок, в связи с чем они ограничиваются [2]:
– касательные напряжения в бетоне стенки, вызываемые действием поперечной силы и кручением, которые снижают трещиностойкость балок, в связи с чем они ограничиваются [2]:
, |
(3.50) |
где  – коэффициент условий работы,
– коэффициент условий работы,  = 1,15 [2, п. 3.27];
= 1,15 [2, п. 3.27];  – расчетное сопротивление бетона скалыванию при изгибе, принимаемое по [2, табл. 23,
– расчетное сопротивление бетона скалыванию при изгибе, принимаемое по [2, табл. 23,
с. 35].
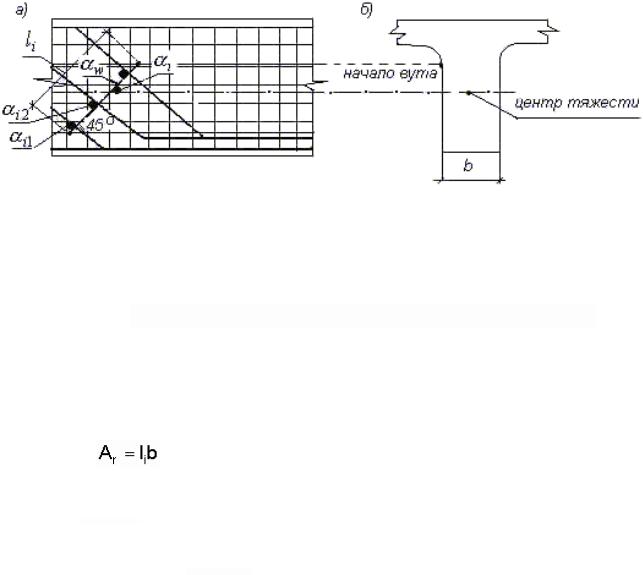
Рис. 3.10. Схема для определения ширины раскрытия наклонной трещины: а
– вид вдоль оси балки; б – поперечное сечение балки
Радиус армирования наклонного сечения определяется [2]:
(3.51)
где  – площадь зоны взаимодействия арматуры с бетоном для наклонного сечения, определяемая по формуле:
– площадь зоны взаимодействия арматуры с бетоном для наклонного сечения, определяемая по формуле:
, |
(3.52) |
где  – длина наклонной трещины (рис. 3.10);
– длина наклонной трещины (рис. 3.10);  – ширина балки пролетного
– ширина балки пролетного
строения;  – коэффициенты, учитывающие степень сцепления с бетоном соответственно наклонных стержней (отгибов), ветвей хомутов и
– коэффициенты, учитывающие степень сцепления с бетоном соответственно наклонных стержней (отгибов), ветвей хомутов и
продольных стержней;  – число наклонных стержней, ветвей хомутов и
– число наклонных стержней, ветвей хомутов и
продольных стержней в пределах наклонного сечения длиной  ;
;  – диаметры наклонных стержней, ветвей хомутов, продольных стержней;
– диаметры наклонных стержней, ветвей хомутов, продольных стержней;
 – см. формулу (3.49).
– см. формулу (3.49).
3.1.8. Программное обеспечение расчетов балки железобетонного пролетного строения
Для расчета элементов железобетонного пролетного строения из ненапрягаемой арматуры разработан пакет прикладных программ Rashet JB для использования на персональном компьютере. Он состоит из четырех модулей, работающих автономно: Powers. exe, Most. exe, 92. exe, 93.exe.
Структура программных модулей представлена на рис. 3.11.
