
- •1. Основные направления методологии научного исследования.
- •2. Определение научного метода.
- •3. Этапы научного исследования.
- •4. Принципы научного исследования.
- •5. Типы научного исследования.
- •6. Отличия критического исследования от поискового и воспроизводящего.
- •7 Вопрос. Научная теория, ее структура и функции.
- •8 Вопрос. Проблема и гипотеза.
- •9 Вопрос. Выбор темы научного исследования
- •10 Вопрос. Изучение научной литературы
- •11 Вопрос. Методологические аспекты исследования малой группы
- •12 Вопрос. Логика научного исследования.
- •Вопрос 13 Проблема и тема исследования
- •Вопрос 14 Объект и предмет исследования
- •Вопрос 15 Цели и задачи исследования
- •Вопрос 16 Гипотеза
- •Вопрос 17 Этапы исследования
- •Вопрос 18 Личностные качества психолога-практика
- •19. Классификация методов психологического исследования Классификация методов психологического исследования.
- •20. Эмпирические методы в психологическом исследовании
- •21. Личность и деятельность эксперементатора.
- •22. Личность испытуемого и его деятельность в псих эксперименте.
- •24. Планирование эксперимента.
- •25. Основные эксперементальные планы
- •26. Взаимодействие независимых переменных, виды взаимодействия.
- •27. Корреляционное исследование и его планирование. Понятие признаков и переменных.
- •28. Шкалы измерения.
- •29. Распределение признака. Параметры распределения. Понятие о нормальном распределении
- •30. Понятие статистических гипотез.
- •31. Статистические критерии: параметрические и непараметрические, их возможности и ограничения.
- •Понятие о статистическом критерии
- •Уровень значимости и мощность
- •Состоятельность и несмещенность критериев
- •32. Понятие уровней статистической значимости.
- •4. Обсуждение результатов.
- •36. Представление результатов исследования
- •37. Использование таблиц, графиков, диаграмм эмпирического исследования в области практической психологии
29. Распределение признака. Параметры распределения. Понятие о нормальном распределении
Нормальный закон распределения играет важнейшую роль в применении численных методов в психологии. Он лежит в основе измерений, разработки тестовых шкал, методов проверки гипотез. История применения закона нормального распределения в социальных и биологических науках начинается, по-видимому, с работы бельгийского ученого А. Кетле «Опыт социальной физики» (1835 г.). В ней он доказывал, что такие явления, как продолжительность жизни, возраст вступления в брак и появления первого ребенка и т. д., подчиняются строгой закономерности. Она проявляется в том, что чаще всего встречаются средние значения соответствующих показателей, и чем больше отклонение от этой средней величины, тем реже встречаемость таких отклонений. Одинаковые отклонения от среднего в меньшую и в большую сторону встречаются одинаково реже, чем среднее значение. Эту закономерность он назвал «законом уклонения от средней величины». В его исследованиях, и позднее – в исследованиях англичанина Ф. Гальтона, было доказано, что распределение частот встречаемости любого демографического (продолжительность жизни и пр.) или антропометрического (рост, вес и пр.) показателя, измеренного на большой выборке людей, имеет одну и ту же «колоколообразную» форму (рис. 6.1).
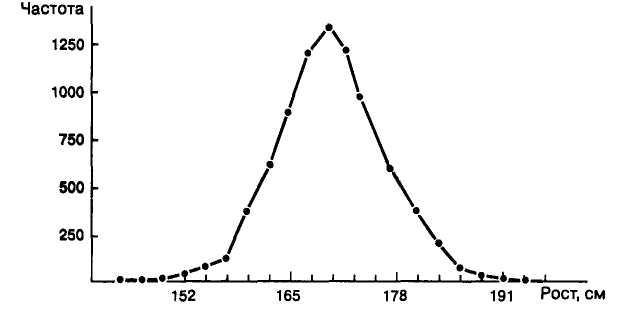
Рис. 6.1 Полигон частот для роста 8585 взрослых людей,
родившихся в Англии в XIX в.
Форма таких распределений может быть описана математической формулой, которую предложил еще в XVIII веке математик де Муавр.
Де Муавр решал следующую задачу. Предположим, монета в азартной игре подбрасывается 10 раз, и каждый раз она может с равным успехом выпасть «орлом» или «решкой». Какова вероятность того, что в результате этой игры выпадет 0 «орлов», или 1 «орел», ..., 10 «орлов»? Сложные вычисления дают математически точное решение такой задачи (рис. 6.2). А если игра состоит из 100 подбрасываний монеты, или 1000? Де Муавру удалось доказать, что уравнение кривой, соединяющей вершины отрезков на рисунке 6.2, для данного случая или для любой другой подобной задачи имеет следующую формулу:
![]() ,
(6.1)
,
(6.1)
где f(хi) − высота подъема кривой, е − основание натурального логарифма (примерно 2,718), π − число «пи» (примерно 3,14), М и σ − среднее и стандартное отклонения для переменной хi, которые определяют положение кривой на числовой оси и задают ее размах. Эта формула и соответствующая ей кривая (рис. 6.2) впоследствии получили название закона нормального распределения. Итак, исход азартной игры, и продолжительность жизни, и рост человека − все это случайные события, частота (или вероятность) встречаемости которых подчинена закону нормального распределения. А. Кетле объяснял это существованием «идеала» человеческой природы, которому соответствуют средние значения различных показателей.
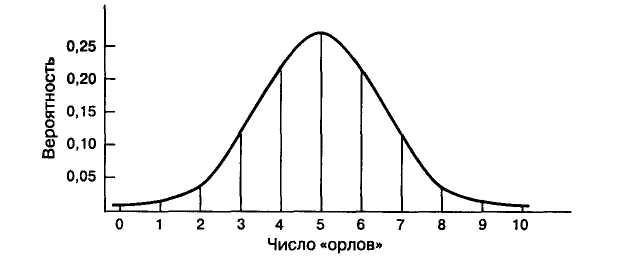
Рис. 6.2. График распределения вероятностей выпадения «орлов»
в игре с 10 подбрасываниями монеты и кривая нормального
распределения
Ф. Гальтон, двоюродный брат Ч. Дарвина, проявление нормального закона рассматривал в связи с биологической изменчивостью, наследственностью и отбором. В дальнейшем трудами Ф. Гальтона и его последователей было доказано, что и психологические особенности, например, способности, подчиняются нормальному закону. Поэтому дальнейшее развитие измерительного подхода в психологии и статистического аппарата проверки гипотез происходило на базе этого общего закона.
Подведем важный итог этого краткого исторического экскурса. Начиная со второй половины XIX столетия измерительные и вычислительные методы в психологии разрабатываются на основе следующего принципа. Если индивидуальная изменчивость некоторого свойства есть следствие действия множества причин, то распределение частот для всего многообразия проявлений этого свойства в генеральной совокупности соответствует кривой нормального распределения. Это и есть закон нормального распределения.
Закон нормального распределения имеет целый ряд очень важных следствий, к которым мы не раз еще будем обращаться. Сейчас же отметим, что если при изучении некоторого свойства мы произвели его измерение на выборке испытуемых и получили отличающееся от нормального распределение, то это значит, что либо выборка нерепрезентативна генеральной совокупности, либо измерения произведены не в шкале равных интервалов.
